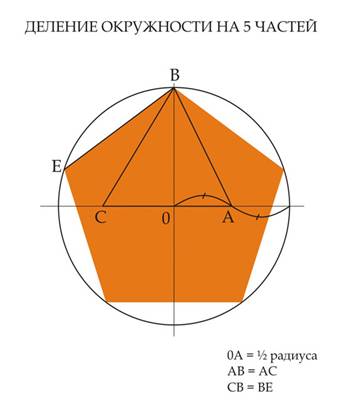
|
Андрей Чернов. Заметки о вечном. SECTIO AUREA. ИМЯ, ДАННОЕ ПО ОШИБКЕ (3) ЗОЛОТО НЕДР И ЗОЛОТО НЕБА Сегодня золотое сечение уже не воспринимается как чудо (за ним можно ходить, как по грибы после июльского дождика). Но если даже вы наберете целую корзину нечервивых примеров, ни один новостной канал об этом не сообщит. Может сложиться представление, что золотое сечение – игрушка для маргиналов и провинциалов от науки (что-то вроде фоменковско-носовской «новой хронологии»), и наука сама по себе, а златоделы – сами с усами (то ли масонская ложа, то псевдонаучная секта, в которой все всех давно знают, где читают и почитают только друг друга и время от времени заявляют о новых глобальных открытиях, остающихся, впрочем, неизвестными для непосвященных, то есть для всех прочих). Но сказать, что наследники Фибоначчи разрабатывают золотую жилу, – не повернется язык: кроме головной боли и недоумения ближних на этих приисках мало что можно заработать. И хотя члены «золотого клуба» изрядно постарались для снижения уровня собственной научной репутации, и в этом хоре подчас раздаются голоса, звучащие не только респектабельно, но и вполне убедительно. Сотрудник Пущинского научного центра РАН В. Д. Цветков показал, что «у млекопитающих оптимальная деятельность сердца обусловлена максимальной экономичностью его конструкции. Энергетическая оптимизация сердца обусловлена золотым сечением и числами Фибоначчи. Золотые отношения составляют основу законов композиции структур сердечного цикла; эти соотношения справедливы для различных видов млекопитающих»[1]. В 2002 г. к выводу о том, что «в теории электрослабых взаимодействий возникают отношения, приближенно совпадающие с золотым сечением» пришел известный российский физик-теоретик проф. Ю. С. Владимиров (кафедра теоретической физики Московского университета). Впрочем, обнаружение новых примеров золотой пропорции в тех или иных явлениях уже мало что добавляет к известному. Всем ясно, что золотое число – некая гармоническая константа. А потому, прежде чем говорить о золотой пропорции, надо попытаться сформулировать, а что же такое сама гармония. Заметим, что сейчас нас интересует не философское, а именно технологическое определение. ЗА ЧТО ПОГИБ ГИППАС ИЗ МЕТАПОНТА? Языческий мир архаики был страшен и дробен. Пифагорейцы склеили его числом и одушевили понятием целостности. Оказалось, что микро- и макрокосмос подчиняются одним законам, потому и едины. Этот единый мир повиновался гармонии, в нем над всеми войнами и бедами победно звучала лишь одна музыка – музыка сфер. В VI веке до н. э. Пифагор полагал, что гармония – высший мировой закон, выражающийся в примирении первичных противоположностей (к примеру, границы и безграничного). И потому само существование вселенной – постоянное ограничивание неограниченного, а познание – определение неопределенного. Эта парадигма и лежит в основе той цивилизации, которую зовут европейской. Как же Пифагор Самосский пришел к своим столь парадоксальным выводам? Все началось с теоремы Пифагора (считается, что ученый привез ее из Египта или Вавилона) и открытия квадратного корня из 2. Древним египтянам был известен целочисленный прямоугольный треугольник со сторонами 5–4–3. Его обычно называют священным египетским треугольником. Строители и археологи им пользуются и сегодня: чтобы заложить котлован или раскоп, достаточно последовательно отметить на веревке отрезки в 5, 4 и 3 метра и по этим отметкам сложить из веревки треугольник: угол между двумя меньшими сторонами всегда будет прямым[2]. Но когда Пифагор осознал, что сумма квадратов катетов равна квадрату гипотенузы (вспомним школьный стишок «Пифагоровы штаны в обе стороны равны»), он стал жертвой собственного прозрения. Напомним, что квадратный корень из целого числа есть число, которое надо умножить само на себя, чтобы получить данное целое число. Большинство квадратных корней выражаются бесконечной непериодической десятичной дробью. (Исключение – целые числа, которые представляют собой квадраты других целых чисел; так четверка равна квадрату двойки, а 9 = 32). Квадратные корни с бесконечной десятичной дробью и числа, полученные на их основе, с легкой руки Пифагора были названы иррациональными. √2 = 1,4142136... и т. д.
√5 = 2,236086...
Священный египетский треугольник и Пифагоровы штаны Иррациональность (несоизмеримость) отношения √2 : 1 доказывалась тем, что квадрат, построенный на диагонали меньшего квадрата, в два раза больше исходного квадрата. Из теоремы Пифагора следовало, что если сторону квадрата принять за единицу, то длина диагонали будет равна √2. Но ни одна состоящая из двух целых чисел простая дробь a/b при возведении «в квадрат» двойку не дает. Значит, существует некий бесконечный класс тайных иррациональных чисел, невыразимых ни целыми числами, ни их отношениями. И если сторону квадрата принять за единицу, то сторона квадрата просто несоизмерима с его диагональю, которая будет равна невыразимому при помощи целых чисел (или их отношения) иррациональному числу √2. Это открытие и потрясло философа[3]. Иррациональность (по-русски можно сказать – заумь) пугала, ведь арифметика Древней Греции – арифметика целых чисел. Аристотель в «Метафизике» поучал: «Число есть множество, которое может быть измерено единицей». Ему вторил Евклид во втором определении VII книги «Начал»: «Число же – множество, составленное из единиц». То, что диагональ квадрата несоизмерима с его стороной, как казалось самому Пифагору, было вызовом тому миропорядку, который античный философ и считал разумно расчисленным Космосом. Пифагор засекретил свое открытие, поведав о проблеме иррациональности лишь ближайшим ученикам, среди которых первым был Гиппас из Метапонта. «...рассказывают, что пифагореец Гиппас, виновный в письменном изложении учений Пифагора в ясной форме, был изгнан из школы и ему как будто умершему, был поставлен надгробный столб» – пишет древний автор. Это значит, что, казалось бы, преодоленная архаика вовсе не собиралась сдаваться. Основа гармонии, число, понятое как целая, положительная и натуральная сущность, вне иррациональных величин гармонии не описывало. И та была принесена в жертву рациональной ясности. (Что-то подобное произойдет через две тысячи лет на переходе от средневековья к гуманизму.) Для себя пифагорейцы допускали, что иррациональное имеет такие же (если не большие) права на участие в строительстве мироздания. Но только для себя. Вина Гиппаса заключалась в том, что он разгласил непостижимую по
самой своей природе иррациональную тайну диагонали квадрата («открыл
недостойным участия в учениях природу пропорции и несоразмерности»). Гиппас
был изгнан из тайного ордена пифагорейцев, и вскоре наказан богами (погиб при
кораблекрушении).
Попирая принципы авторского права (или, во всяком
случае, право автора на сохранение своего открытия в тайне), Гиппас
Метапонтийский подражал Прометею. Сходство усиливается еще одним
обстоятельством: Гиппас, если верить Аристотелю, учил, что первоэлемент всего
сущего – огонь и что души также имеют огненную природу. И именно Гиппасу мы обязаны
открытостью и демократичностью античной, а потом и европейской науки.
Пифагорейцы зря боялись дискредитации собственного метода. Пройдет несколько десятилетий и разглашенная Гиппасом тайна иррационального следующим поколениям покажется простой и естественной. Проблема несоизмеримости перевернула архаические представления о космосе. В диалоге Платона «Законы» некий афинянин жалеет, что поздно узнал о несоизмеримости и стыдится того, что не знал об этом раньше, ибо «это свойственно не человеку, но скорее каким-то свиньям» Вот и Аристотель в «Топике» утверждает, что «удовольствию от питья противоположно страдание от жажды, но удовольствию от рассмотрения того, что диагональ несоизмерима со стороной, ничего не противоположно». Как именно сумел античный гений перебороть кризис сопряжения меры и несоизмеримости? Да очень просто: греки построили Парфенон и сами себе предъявили ту красоту, ту гармонию, которая и возникает в пограничной зоне между рациональным и ирррациональным. Они обожествили то, что не поддается разумению. Аморфное тело (представим себе, к примеру, горный пейзаж), разрушаясь, может стремиться лишь к тому, чем наделены простейшие структуры, к примеру, кристаллические, – к симметрии. Чем больше пройдет времени, тем покатей и симметричней станет превращающаяся в холм гора. Но если мы имеем дело с самоорганизующейся и самоперестраивающейся системой (это может быть физическое тело или явление, это может быть и субъект эволюционирующего биологического вида), то в ее основе должны лежать какие-то структурообразующие точки, или, скажем, точки гармонической кристаллизации. Точки
синтеза в естественных гармонических системах обусловлены пропорцией,
эволюционно заданной разноприродными гармоническими константами – корнями из
пятерки и двойки, золотым сечением и числом π. Итак, под синтезом разноприродного мы будем понимать пропорциональное взаимодействие целочисленного с иррациональными (золотое сечение, его функции, √5, √2) и трансцендентными (или, как однажды выразился писатель Андрей Синявский, – потусторонними) гармоническими константами. (Впрочем, в последнем случае мы ограничимся несводимым к квадратным корням числом π). Квадратные корни – это геометрическая симметрия прямого, а трансцендентное π – то, что объединяет круглое (окружность) с прямым (диаметр) и является основой синусоиды, то есть любого циклического процесса. Но гармония квадрата (или круга) не в симметрии, а в несоизмеримости стороны (или длины окружности) с диагональю (или диаметром). Словом, как заметил еще Козьма Прутков, – зри в корень. В нашем случае – в квадратный. ПАРОЛЬ ПИФАГОРЕЙЦЕВ Простая симметрия слишком скучна (можно сказать – мертва), и умение разделить отрезок так, чтобы он жил, в древности казалось приобщением к небесному знанию. Вслед за Пифагором правильные десяти- и пятиугольники строил в Александрии в III веке до н. э. Евклид. А почти через две тысячи лет Альбрехт Дюрер в своем «Руководстве к измерению» привел свой способ построения пентаграммы.
В переводе
с греческого пентаграмма значит «пять линий». Родом она из Вавилона, и
возраст первых пентаграмм, найденных на глиняных табличках, около трех
тысяч лет. В живой природе широко распространены
формы, основанные на пентагональной симметрии. Это, к примеру, многие морские
звезды и морские ежи. У человека на каждой руке и ноге по пять пальцев, пять
лепестков у цветов кувшинки, шиповника, боярышника, гвоздики, груши,
черемухи, яблони и земляники. Число 5 у пифагорейцев обозначало брак и богиню
рождения Афродиту, ведь пятерка – результат сложения двойки первого женского
(четного) числа и тройки первого мужского (нечетного) числа. Любовь и
дружество выражались числом 8 (ибо что может полнее выражать гармонию, чем октава?)[4]. Десятка же была числом Вселенной (1+2+3+4). Исходя из
этого, пифагорейцы считали, что количество небесных сфер должно быть также
равно десяти, а поскольку их насчитали только девять (сферы неба, Солнца,
Луны, Земли, Меркурия, Венеры, Марса, Юпитера и Сатурна), на кончике пера
была «открыта» вращающаяся по десятой сфере планета Антихтон (Противоземля). Считается, что в Грецию звездчатый пятиугольник привез из Египта или Вавилона тот же Пифагор. Решив задачу о делении окружности на пять равных частей, пифагорейцы сделали пентаграмму тайным паролем своего сообщества. Но у красивого равенства соотношений длинных и коротких отрезков пентаграммы нет целочисленного выражения, а пифагорейцы признавали числом лишь то, что состоит из единиц (то есть только целые положительные числа). Пифагорейцы, конечно, должны были заметить, что в правильной пентаграмме (то есть звезде) любой отрезок находится в золотом отношении с меньшим соседним. Надо думать, Гиппас из Метапонта был казнен греческими богами еще и потому, что мог выдать грекам (или даже выдал) и другую алогичную и страшную тайну – тайну пентаграммы (в основе которой лежит √5).
В звездчатом пятиугольнике каждая из
пяти линий, составляющих эту фигуру, делит другую в отношении золотого
сечения, а концы звезды являются золотыми треугольниками. Но золотой треугольник весьма близок к священному египетскому треугольнику 5-4-3, на котором строилась древнейшая «вавилонская» (неправильная) пентаграмма. Кто из древних и когда превратил «вавилонскую» пентаграмму в золотую, мы пока не знаем. ЗАМЕТКИ
НА ПОЛЯХ Угол каждого из лучей пентаграммы 36°. Прямоугольный треугольник с углом в 36° очень близок к священному
египетскому (но не равен ему). И если у египетского треугольника отношение сторон
5:4:3, то здесь отношение углов 5:3:2 (соответственно 90º, 54º и
36º). В таком треугольнике гипотенуза относится к большому катету как
двойное минорное золото к единице (√5 –1 к 1), а, значит:
Ф : 2 = Cos 36°
Отсюда следует формула, связывающая
золотую пропорцию с числом π : √5 + 1 π
Ф = ––––––– = 2 Cos –– 2 5 И эта связь драгоценна, ведь число
π – основа синусоиды, а, значит, любого гармонического процесса. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. В средние века пентаграмма предохраняла от «нечистой силы». И за это считалась «лапой ведьмы» (по аналогии со следом звериной лапы). Вспомним, как сказано у Гёте (и его переводчика Николая Холодковского): Мефистофель: Нет, трудновато выйти
мне теперь. Волшебный знак у
вашего порога. Фауст: Не пентаграмма ль
этому виной?.. Но как же, бес,
пробрался ты за мной? Каким путем впросак
попался? Мефистофель Изволили её вы плохо
начертить, И промежуток в уголку
остался, Там, у дверей… «Промежуток в уголках» – это и есть
неправильная «вавилонская» пентаграмма. Разделить окружность на пять или
десять частей куда труднее, чем на три или шесть.
Правильный звездчатый пятиугольник самим своим видом говорил о том, что должно существовать число, описывающее его пропорции. Но хвост этого числа уходил в самые недра тартара. Пушкин в таких случаях писал: «Как человек с предрассудками я оскорблен…». Должны были пройти столетия, чтобы математики научились в числе видеть не только рациональную утопию, но и иррациональную реальность мира. Лука Пачоли писал: «...наша священная пропорция, согласно Платону в его “Тимее”, дает формальное бытие самому Небу, ибо ему приписывается вид тела, называемый додекаэдром, который невозможно построить без нашей пропорции». Додекаэдр – одно из «Платоновых тел», правильных многогранников, описанных Платоном. Правильных многогранников всего пять – тетраэдр (четырёхгранник), куб (шестигранник), октаэдр (восьмигранник), додекаэдр (двенадцатигранник) и икосаэдр (двадцатигранник). Это выпуклые максимально симметричные объекты, у которых все грани – правильные многоугольники, а в каждой вершине сходится одинаковое число граней и все двугранные углы равны. У куба грань – квадрат, у додекаэдра – пентаграмма, у трех прочих Платоновых тел грани представляют из себя правильные треугольники. У пифагорейцев каждое из Платоновых тел символизировало одну из пяти стихий – огонь, землю, воздух, воду, эфир. Вслед за своим учителем они полагали, что огонь и возник из тетраэдра, земля из куба, воздух из октаэдра и т д.
Две тысячи лет спустя на исходе средневековья рассчитать механику Солнечной системы при помощи Платоновых тел попытается Иоганн Кеплер. Он будет полагать, что Солнечная система – это ряд последовательно вложенных друг в друга правильных многогранников. Остается лишь пожалеть о том, что это всего лишь красивая сказка: современная наука этой гипотезы Кеплера, увы, не подтверждает. Окажись Кеплер прав, как все было бы просто и ясно! (Остается полагать, что Демиург отверг этот красивый но простой путь, поскольку он не обеспечивал единства и гармонии на каком-то другом, более высоком уровне.) Утешимся тем, что 12 ноября 1984 года в
международном журнале «Physical Review Letters» израильский физик Дан
Шехтман опубликовал экспериментальное доказательство существования
металлического сплава с икосаэдрической кристаллической структурой. Речь шла
о запрещенной классической кристаллографией симметрии Пятого порядка. Сплавы
со свойствами сплава Шехтмана были названы квазикристаллами. В
посвященной этому открытию статье Д. Гратиа «Квазикристаллы» («Успехи
Физических Наук», 1988), говорилось,
что «его значение в мире минералов можно поставить в один ряд с добавлением
понятия иррациональных чисел в математике». Утверждают, что природа не знает ни
правильного треугольника, ни квадрата. Однако это не так. Если поместить в
жидкость в сосуд с вращающимся дном (и неподвижными стенками), то при разной
скорости вращения дна на (прямо по центру) поверхности возникнет треугольник
или квадрат – базовые фигуры Платоновых тел.
Однако Платоновы тела – только часть этой, покуда не объясненной самогармонизации материи. Как сообщил официальный сайт NASA, космический аппарат Cassini передал снимки северного полюса Сатурна, на которых видно изображение необычного образования в форме шестиугольника (гексагона)[5]. Более двадцати лет назад сходная структура была обнаружена
аппаратами Voyager 1 и Voyager 2. Ширина шестиугольника равна 25 тысячам
километров (на его поверхности поместятся два земных шара), а прямые стены
вихря уходят вниз на Снимки, переданные Cassini, делались, начиная с октября 2006 года, с помощью инфракрасного спектрофотометра. (До этого времени северный полюс Сатурна находился под покровом пятнадцатилетней полярной ночи.)
Северный полюс Сатурна. Снимок NASA Гексагон – это максимально симметричный многоугольник, известный и по многим земным образованиям – таковы снежинки, молекула бензола, пчелиные соты, раскрытый бутон тюльпана. Причем, обратим внимание: мы видим не один шестиугольник, а серию этих фигур, вложенных друг в друга. Итак, на северном полюсе Сатурна, жидкой планеты-гиганта,
материя «кристаллизуется» в виде правильного шестиугольника. Шестиугольный (а
не круглый) сатурианский вихрь говорит о том, что и в природных объектах
геометрия прямого (скажем, пропорция сторон и диагоналей) может
реализовываться столь же последовательно, как и геометрия круглого. В Интернете можно найти упоминания о проводившихся в Дании опытах с так называемым «Ведерком Ньютона». Это обычный цилиндрический сосуд с водой, у которого электромотор вращает лежащий на дне круглый плексигласовый диск. При разных скоростях вращения на поверхности воды появляются геометрические фигуры – треугольник, квадрат, пятиугольник, шестиугольник. Но именно пятиугольник оказывается наиболее устойчивой фигурой.
Пятиугольник в «Ведерке Ньютона». ВСЕМИРНЫЙ ПОТОП ПРОДОЛЖАЕТСЯ? В отличие от
золотого сечения √2 обделен вниманием исследователей. Дружат
с ним лишь архитекторы да производители писчей бумаги: европейский стандарт
листа любого формата √2 к 1. Проиллюстрируем на модели Земли, как в паре, душа в душу, трудятся во благо гармонии золотая пропорция и скромный √2. В околонаучной литературе и в интернете можно найти десятки самых экзотических попыток связать золотое сечение с параметрами нашей планеты. В одних случаях для получения «золотого результата» нам предлагается произвести ряд сложных математических преобразований, в других можно прочитать, скажем, такое: «Поверхность Земли покрыта водой и сушей неравномерно. Площадь океанов занимает 62% ее поверхности, остальное – материки и моря. Вряд ли это, случайное соотношение двух основных образований – литосферы и гидросферы, определяющих вид, рельеф и геоморфологическую жизнь на планете. Оно отвечает Золотой Пропорции. За долгий период эволюции, структура планеты должна была достичь оптимальных значений»[6]. 62% – это золотое сечение от 100%. Но в любой энциклопедии мы прочтем, что около 58% земной поверхности приходится на глубоководные (3–5 км) океанические бассейны, а 13% – на довольно мелководный континентальный шельф и переходные области. 58 + 13 – это 71, а не 62. Да и каким скальпелем можно отделить Баренцево море от Северного Ледовитого океана, а Аравийское от Индийского? И как определить границы Саргассова моря, которое находится посредине Атлантического океана и названо по скоплению на его поверхности кочующих по водной глади саргассовых водорослей? Покажем, что в подобных подгонках под ответ просто нет нужды. Реальность куда интересней. Площадь поверхности Земли 510 072 000 км2. Сегодня 361,132 миллионов квадратных километров – океан, а 148,94 миллиона – суша[7]. Отношение всей поверхности нашей планеты к поверхности мирового океана 1,4124, что меньше √2 лишь на 0,0018. И, если бы мы не знали, что приближение к √2 – следствие одной из двух эволюционных формул, то наверняка сочли бы такое «странное сближение» простым совпадением. Но условно поверим, что это некая реализованная в геометрической модели физическая закономерность и проверим это предположение. По формуле √2 океан в «идеальном случае» должен занимать 360,675 миллионов км2. Площадь мирового океана в начале XXI столетия на 456,63 тысяч км2 больше того, что можно назвать формульной нормой[8]. Диаметр экватора 40 тысяч км., а, значит, из «недостающей» территории можно было бы скроить ленту шириной в десять километров и перепоясать ею Земной шар. (Очертания материков при этом, конечно, изменятся, но столь незначительно, что на школьном глобусе это будет практически незаметно.) От земных горизонталей поднимемся к вертикалям. Но сначала краткое предуведомление. Было бы бессмыслицей искать корреляции, скажем, между максимальными вершинами разных материков или протяженностью великих рек. Поговорка «в огороде бузина, а в Киеве дядька» в привычном своем смысле не работает лишь в том случае, когда бузина и растет в огороде этого самого дядьки. Поэтому будем сравнивать лишь те параметры, которые, как в классицистической трагедии, обусловлены рамками единого места, времени и действия. Скажем, максимум осадков выпадает в предгорьях Гималаев – в среднем это 12 660 мм/год. Но зарегистрированный пик – 23 000 мм/год[9]. Пропорция среднего значения к его превышению: 12 660 : 10 340 = 1,224 →
√5 – 1 Еще пример. В северном полушарии Максимальная температура на Земле в тропических пустынях +58,1 С° (Триполи, Северная Африка). А минимальная температура, зарегистрированная в том же северном полушарии, –71 С° (Оймякон)[10]. 71 : 58,1 = 1,222 → √5 – 1 Максимально низкая температура в Антарктиде (-89,2 С°). Разница с Триполи 147,3 С°: 147,3 : 89,2 = 1,65 → Ф Это значит, что в Антарктике возможно падение термометра и до отметки 91,04 ° С Или в Триполи может быть на пару градусов жарче (в обоих случаях пропорция будет золотой). Но брать для сравнения максимально низкую температуру во Франции было бы некорректно. ЗАМЕТКИ
НА ПОЛЯХ Эверест,
он же Джомолунгма (по-гималайски «Крыша Мира») достигает 32 500 м : 19881 м = 1,63 → Ф Значит, величина перепада поверхности нашей планеты увязана с мощностью внешней твердой оболочки Земли по мажорному золоту (1,618...). Под горными массивами земная кора толще, чем под материками (и куда толще, чем под океанами). Среднее между максимумом и минимумом материковой коры 52,56 км. Сравним со средним значением всей коры: 52 560 м : 32 500 м = 1,617 → Ф
Но большинство пропорций в перепадах земной коры – пропорции, близкие к числу двойного минорного золота. В утрированном виде профиль суши и дна мирового океана образует две гигантские «ступени» – океаническую и материковую. Вторая поднимается над первой в среднем на 4670 м (усредненная высота суши 875 м; средняя глубина океана 3795 м). Пропорция перепада высот дна и суши к среднему уровню дна: 4670 м : 3795 м = 1,231 → √5
– 1 Однако приближение к той же пропорции двойного минорного золота (√5 – 1) мы находим и в максимальных (относительно нуля поверхности океана) перепадах поверхности земной коры: 11033 м : 8848 м = 1,247 → √5
– 1 Вот и высота Эвереста над современной нулевой отметкой океана к глубине впадины (взятой от океанского дна) также даст приближение к двойному минорному золоту: 8848 м : 7238 м = 1,222 → √5
– 1 Величина 4670 м (перепад ступеней) от уровня океана не зависит. И если средние высоты определены с верно, значит, по золотой формуле уровень воды в Мировом океане должен быть снижен на 43 метра. На нашем чертеже эта величин равна толщине линии, разделяющей поверхность океана и атмосферы. Но поскольку, как писал поэт, «Если где-то нет кого-то, значит кто-то где-то есть», а площадь Мирового океана относится к площади суши как √2 + 1 к 1, изъятая из океанского обращения вода ляжет в виде ледового покрова на континенты. И толщина континентальной ступени возрастет примерно на 104 м[12]. Представим, что уровень океана упал и максимальная глубина Марианской впадины уже не 11033, а 10990 м. Тогда и Эверест, не увеличиваясь ни на миллиметр, становится на те же 43 метра выше. И пропорция на глазах позолотеет: 10990 м : 8891 м = √5 – 1 Идеальный (с точки зрения
формулы) уровень Мирового океана должен быть на 43 м ниже существующего (10990 : 8891 = √5 – 1). Тогда
толщина материковой ступени (вместе с ледниками) будет 4774 м, а от нулевой
отметки до дна океана окажется 3752 м: 4774 м : 3752 = 1,272 Это практически число квадратуры круга (отношение площади
квадрата к площади вписанной в него окружности) 4/π = 1,273. Число π возникает и в другой земной пропорции.
Поделим абсолютный перепад высот земной коры на взятую от средней глубины
мирового океана высоту Эвереста: 19881 : 12643 =
1,572 При π/2 = 1,571.. Значит, скорректировав высоту Мирового океана, мы получили вполне определенную тенденцию, обусловленную равновесностью золотой пропорции и числом π. Мы не знаем, какими физическими механизмами обусловлено
приближение пропорций к той или иной гармонической константе, но можем
констатировать, что такое приближение – ясно выраженный феномен вертикальных
пропорций земной коры. Каким-то непостижимым образом уровень океана оказывается именно таким, чтобы стать нулем для пропорционального золотого отсчета отношения уровня усредненной суши, уровня усредненного дна, глубины Марианской впадины, а также для пропорции максимальной земной высоты и максимальной глубины. И все это подтверждается формулой идеального (с точки зрения пропорционального золота) отношения всей земной поверхности к поверхности современного океана А эта формула нам и сообщила, что уровень воды на Земле, судя по отклонению от константы √2, сегодня чуть выше «идеального». Что, впрочем, и понятно, поскольку мы живем во время теплого климатического периода, а уровень океана понижается лишь в ледниковые эпохи, когда огромные массы воды концентрируются на континентах в виде льда и снега. Перепад в
43 метра – катастрофа для цивилизации. И, видимо, известный многим народам
мира миф о Всемирном потопе – из той же постледниковой купели. К такому
выводу пришел действительный член
Русского Географического общества РАН Вячеслав
Кудрявцев[13]. По египетскому преданию, изложенному Платоном в диалогах «Тимей» и «Критий», Атлантида – гигантский остров в Атлантике за Геркулесовыми Столпами, погибший около 12 тысяч лет назад. У Платона сказано «девять тысяч лет назад». Такую дату, ссылаясь на древние манускрипты, называет беседующий с Солоном египетский жрец. По его версии Атлантида погрузилась в морскую пучину после серии страшных землетрясений «в один ужасный день и одну ночь». Но было ли землетрясение? Ведь именно 10-12 тысяч лет прошло с конца последнего для Северного полушария Большого ледникового периода, то есть с того времени, когда на дно ушли сотни тысяч квадратных километров мировой суши. Автор этой гипотезы пишет: «На мой взгляд, самым серьезным аргументом в пользу того, что Атлантида не была измышлена Платоном, является то, что указанные в диалогах время и обстоятельства ее гибели (погружение в морскую пучину), совпадают с данными, безусловно, недоступными Платону, о времени окончания последнего Ледникового периода, и сопутствовавшем ему значительном повышении уровня Мирового океана». Специалист по ледникам профессор М. Г. Гросвальд дал такое заключение на работу Кудрявцева: «Сейчас известно, что деградация ледниковых покровов Северной Америки, Исландии и северо-запада Евразии проходила не плавно, ее ход мог бы быть описан не плавной кривой, а “ступенчатым” графиком, на котором вертикальные участки соответствовали бы этапам быстрого спуска льда в океан. Такие спуски, по крайней мере крупнейшие из них, известные как “События Хайнриха”, были синхронизированы по всей периферии Северной Атлантики, при них за короткие сроки в океан поступали миллионы кубокилометров льда, вызывая скачкообразные поднятия его уровня. Один из известных мне эпизодов быстрого сброса льда в океан имел место как раз около 10 тыс. лет назад. Для низменной суши, в том числе для района гипотетической Атлантиды, именно этот сброс льда (ледниковый сердж) мог быть роковым, вызвав гибельный потоп». А заведующий лабораторией Института океанологии им. П.П. Ширшова РАН, академик РАЕН А. М. Городницкий считает, что гипотеза Кудрявцева – «одна из наиболее перспективных гипотез, которые когда-либо предлагались в связи с Атлантидой». |