Правка 5 мая 2009

Андрей Чернов

ЗОЛОТО ПАРФЕНОНА (2)

глава из книги

О ЧЕМ УМОЛЧАЛ ВИТРУВИЙ

Костромской исследовать золотой пропорции Иосиф Шефтелевич Шевелев на основе √5 составил пропорциональное древо Парфенона[1]. Он утверждает, что, последовательно умножая на 1 : √5, из размера высоты ствола колонны можно получить высоту капители. Ряд выстраивается такой: высота ствола колонны – шаг колонны – диаметр колонны – высота капители.

И действительно, отрезок 9,57 м трижды умноженный на 1 : √5 даст отрезок в 0,856 м, что лишь на 4 мм меньше, чем реальная высота капители.

Однако средние члены (шаг колонны и ее диаметр) также отличаются от ожидаемых.

По формуле Шевелева надо: 9,57 – 4,28 – 1,914 – 0,856 м

А по обмерным планам перед нами ряд: 9,57 – 4,291 – 1,907 – 0,86 м.

Критикуя построения Шевелева, новосибирский архитектор Андрей Радзюкевич пишет:

«Попробуем ответить на такой вопрос – если исходный размер – ширина стилобата, равна 100 футам, то, как из него можно получить размер высоты антаблемента? Судя по схеме дерева пропорций Шевелева, этот размер по прямой ветви получить можно, но неизвестно какие при этом следует использовать пропорциональные коэффициенты. Похоже, что автор тоже этого не знает, так как  приводит эту схему в разных изданиях и нигде не дает никаких пояснений. Можно, конечно, предположить, что высота антаблемента получается как разница между размерами высоты ордера и полной высоты колонны, значения которых у И.Ш.Шевелева определены. В этом случае потребуется целый ряд ”легких движений руки” с циркулем:

1. Определяется высота ствола колонны умножением ширины стилобата на

                                                    1 / (√5 + 1)

2. Определяется нижний диаметр колонн через уменьшение  высоты ствола  колонны  в пять раз;

3.Определяется высота капители через умножение нижнего диаметра колонн на величину

                                                     1 / √5

4. Определяется полная высота колонны путем сложения высоты тела колонны и высоты капители.

5. Определяется высота ордера через коэффициент (1 / √5);

6. Определяется высота антаблемента через вычитание высоты колонны от высоты ордера

Произведя в итоге всю эту массу вычислений, получаем, что высота антаблемента должна быть равна 0,1105573 от исходных ста футов. Проверим это соотношение на точность. Умножив ширину стилобата на полученный коэффициент, получаем размер 3,415 м, который больше расчетного на 11,81 см, т.е. почти на целых 12 сантиметров. <…>

Мало того, что полученный способ неточен. Он чудовищно громоздок…»[2].

На самом деле, все совсем не так страшно и громоздко, как это представлено.  Речь-то всего-навсего о трех элементарных делениях и одном сложении. Однако настораживает то, что получаемые размеры «гуляют» в обе стороны – они то больше, то меньше ожидаемого, а, значит, на счет неточности целочисленного приближения ошибки не списать.

Уже первое вычисление даст нам отклонение от реального размера в 3 мм.

Второй шаг, впрочем, выправит положение, и диаметр колонны получится ровно таким, каким и должен быть – 1,908 м.

Результат третьего вычисления безукоризнен.

Однако с четвертым шагом происходит и впрямь что-то непонятное. Вместо того чтобы сложить две полученные величины и получить целое (колонна с капителью), мы зачем-то начинаем вычисление заново. Дело в том, что колонна с капителью все же получается на 3 см ниже, чем в натуре (а это в данном случае очень много!).

Пятый шаг – высота ордера. Она по формуле Шевелева на 8 см выше, чем при обмерах.

И, наконец, – высота антаблемента 3,4129 вместо 3,297 м. Здесь Радзюкевич прав: это уже почти на 12 см больше реального.

Перед нами, конечно, не подгонка под ответ, но и не система, а всего лишь некая тенденция, основанная и на том, что пропорция 9/4 дает 2,25, и на том, что само золотое сечение есть функция от √5.

КАК ПРОЕКТИРОВАЛИ ПАРФЕНОН

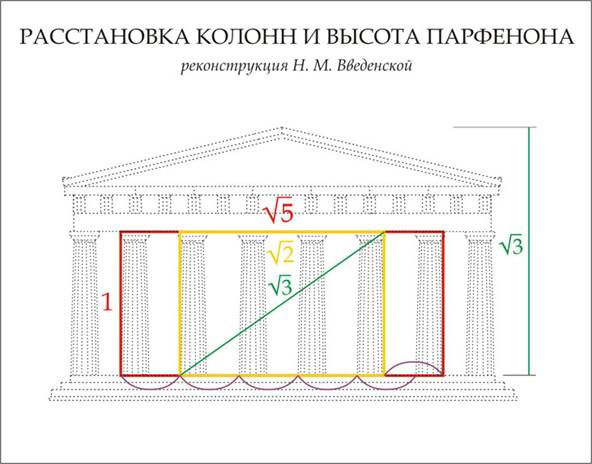
Модуль Парфенона отличается от модуля Витрувия, как алгебра от арифметики. Потому что у замкà, запирающего эту тайну, иррациональная природа. А вот ключи к нему могут быть и натуральными, то есть целочисленными.

Напомню, что иррациональные, и потому и непостижимые для сознания древних √2 и √5 привели к первому кризису античной философии. Поскольку понять иррациональное невозможно по определению, греки обожествили и квадратные корни, и золотое сечение. Наглядное доказательство этого обнаружила искусствовед Н. М. Введенская: стоит вписать в чертеж фасада Парфенона два прямоугольника со сторонами √5 к 1 и √2 к 1, чтобы тут же определить и шаг колонн, и нижний диаметр рядовой колонны, и высоту колонны с капителью.

Нижний диаметр рядовой колонны:

100 оф : 10Ф = 1,908 м

(По плану Баланоса 1,907 м, что можно объяснить эффектом выветривания.)

Шаг рядовой колонны это 100 оф : 10Ф  ∙ 2,25 = 4,293 м

По плану Баланоса средний шаг рядовых колонн 4,295 м, и это говорит об использовании целочисленных отношений при переводе чертежа в камень. Реальный размер пяти шагов рядовых колонн отличается от теоретически рассчитанного лишь на 12 мм (21,476 вместо 21,464 м). При таком алгоритме, скорее всего, вместо Ф использовалось отношение 55/34. (Обозначим его Ф*)

Три шага рядовой колонны + нижний диаметр колонны приравняем к √2.

Пять шагов рядовой колонны + нижний диаметр колонны приравняем к √5.

Это будут горизонтальные стороны наших прямоугольников.

Ну а единица – высота колонны с капителью (10,43 м).

РАССТАНОВКА КОЛОНН И ВЫСОТА ПАРФЕНОНА

Итак, прямоугольник со сторонами √2 к 1 (желтый) вписан в прямоугольник √5 к 1 (красный).

Разница между горизонтальными размерами прямоугольников определит шаг рядовой колонны.

А диаметр рядовой колонны равен остатку после пяти таких шагов.

Диагональ прямоугольника с длинной стороной, равной √2, даст √3. Это и будет высотой Парфенона, взятой от поверхности стилобата.

В натуре при расстановке колонн достигнута удивительная точность: по обмерам пять шагов плюс нижний диаметр колонны дают 23,383 м, а три шага четырех центральных колонн с одним нижним диаметром 14,793 м. Отношение этих величин отличается от отношения √5/√2 лишь на три десятитысячных.

Такого же порядка и определенная, видимо, по целочисленному приближению к √2, (равному 17/12) величина колонны с капителью

Так в середине V в. до н. э., спустя всего полстолетия после смерти Пифагора, проблема иррациональности оказалась не только разрешена, но и воплощена в величайшем из архитектурных шедевров античного мира. Скульптор Фидий вместе с зодчими Иктином и Калликратом самими пропорциями Парфенона словно бы говорили современникам: да, мы не можем понять божественной природы иррационального, но мы научились строить, используя его закономерности. (И за это мы также должны быть благодарны Гиппасу из Метапонта.)

При таком геометрическом построении неясно, как именно высота колонны с капителью связана с шириной стилобата и высотой ордера.

Однако высота ордера, деленная на 29/26 (приближение к √5/2) с точностью до миллиметра дает размер от нулевой отметки до верха капители.

МОДУЛЬ ПАРФЕНОНА

Стилобат – 100 олимпийских футов по 0,30871 м или 63 дорийских локтя по 0,49 м

Высота ордера 100 оф : 2,25 или 28 дорийских локтя

Нижний диаметр рядовой колонны фасада (со второй по седьмую):

100 оф : 10Ф = 1,908 м

Ф – золотое число 1,618…

Шаг рядовых колонн:

Диаметр колонны, умноженный на 2,25 = 4,293 м (в натуре средний шаг 4,295 м )

При высоте колонны с капителью, принимаемой за единицу, три шага колонны + диаметр колонны = √2, а пять шагов колонны + диаметр колонны = √5.

СВЯЩЕННЫЙ ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК 3-4-5

Священный треугольник может быть вписан в чертеж фасада Парфенона несколькими способами. Наиболее интересным, пожалуй, является такой: длинный катет задан высотой ордера (28 дл), а короткий равен 1/3 ширины стилобата (21 дл).

Если поставить этот треугольник на стилобат так, чтобы одна из его вершин коснулась основания угловой колонны (ее нижний диаметр 4 дл), то длинный катет начнется от основания четвертой колонны.

Наличие священных треугольников может и не говорить о способе проектирования. В ряде случаев перед нами, скорее всего, будет лишь дань популярному отношению 3/4. Однако в данном случае графические совпадения слишком красноречивы, чтобы быть просто совпадениями, ведь они определяют ширину первого межколонья и сумму высоты ордера с высотой основания.

ПЛАН ПАРФЕНОНА

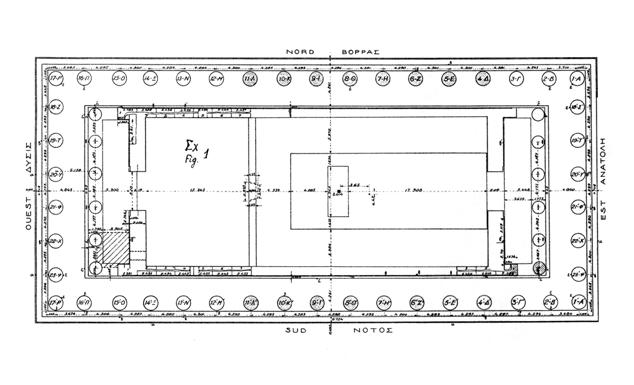
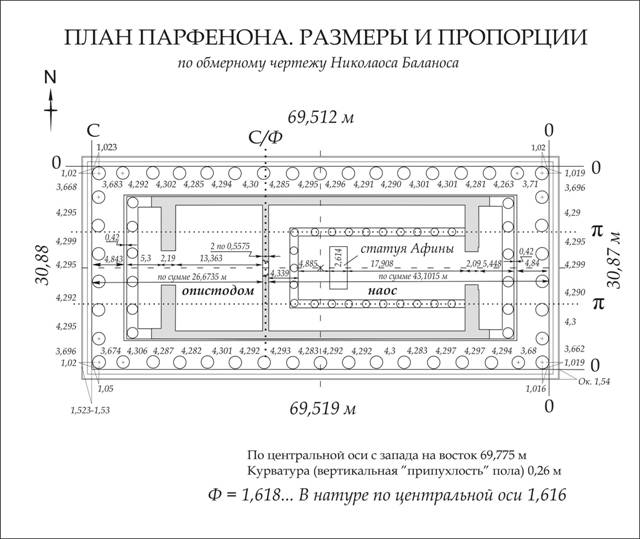
ПЛАН ПАРФЕНОНА ПО БАЛАНОСУ

Святилище поделено на два помещения пропорцией С/Ф (с точностью 1,616).

Ряды колонн внутри святилища расчислены, вероятно, по числу π. Этот же пропорциональный принцип будет заложен и в римской Арке Константина, в церкви Успения в Старой Ладоге середины XII в. и Петропавловском соборе Доменико Трезини.

Все это – лишь геометрия. Как реализовать ее в натуре? Как перевести иррациональные величины, так легко получаемые на чертеже при помощи диагоналей квадратов и полуквадратов, в футы и локти?

Напомним, что древние не умели высчитывать значения квадратных корней, и пользовались или геометрическими построениями, или целочисленными приближениями.

Парфенон это и демонстрирует:

Если ширину стилобата (30,87 м) умножить на √5, то мы получим длину стилобата с отклонением в 48,5 см. Однако заменим √5 целочисленным приближением 9/4, и длина здания будет лишь на 5,6 см более идеального (при размере в 70 метров, да еще с учетом того, что за две с половиной тысячи лет постройка выдержала не одно землетрясение, это вполне приемлемо).

Еще пример: высота карниза 0,6 м; высота архитрава 1,350 м.

0,6 м ∙ √5 = 1,342 м; Откл. 8 мм

0,6 м ∙ 2,25 = 1,35 м; Откл. 0

Значит, мы должны иметь дело с целочисленным приближением к квадратным корням (Таблицу целочисленных приближений к иррациональным константам и более подробный анализ пропорций Парфенона см. в конце этой главы).

Произведем расчет по целочисленному приближению к √2 (17/12) и Ф*, целочисленному (55/34) приближению к числу Ф.

1). Умножаем 100 оф (или 63 дл) на 2,25 и получаем длину стилобата.

2). Делим 100 оф (или 63 дл) на 2,25 и получаем высоту ордера (от верха стилобата до фронтона) 13,728 м[3]

3). Делим 100 оф на 10Ф и получаем нижний диаметр рядовой колонны.

4). Нижний диаметр рядовой колонны, умноженный на 2,25, дает шаг рядовой колонны по ширине стилобата.

По геометрическому построению пять шагов колонны + диаметр колонны должен относиться к высоте колонны с капителью как √5 к 1, а три шага колонны + диаметр колонны к высоте колонны с капителью как √2 к 1.

Как выполнить это условие?

5). Взяли расстояние, занимаемое по горизонтали четырьмя рядовыми колоннами (три шага и толщина одной колонны) и приняли за длинную сторону прямоугольника со сторонами √2 : 1. Поделили на 17/12 (приближение к √2) и получили высоту колонны с капителью – 10,43 м.  Обмер и дает эту величину. (Удвоенная величина колонны с капителью будет относиться к трем шагам колонны по Ф.)

6). Высота ордера, деленная на √2, даст высоту каннелюров (высота ствола колонны с шейкой).

7). Высота каннелюров, деленная на 2,25, даст 4,3236 м. Это 14 оф (4,322 м). Таково и расстояние от верха карниза до верха тела колонны.

Такой, если верить геометрии, должна быть и высота фронтона (также от верха карниза).

8). За нижний диаметр угловой колонны берем сторону модульного квадрата в 4 дорийских локтя. Нижний диаметр угловой колонны, умноженная на 2,25, дает шаг рядовой колонны, но уже по длине стилобата[4].

Однако это лишь начальный этап проектирования. После этого за счет членения антаблемента и прибавления стереобата следует то, что можно назвать «золотой настройкой».

Попытки найти в пропорциях Парфенона золотое сечение регулярно предпринимаются с середины XIX столетия (первым в середине XIX в. был немецкий биолог А. Цейзинг).

А. В. Радзюкевич сообщает:

«По его предположению высота колонн Парфенона в сумме с высотой стилобата относится в ”золотом сечении” к высоте антаблемента в сумме с высотой фронтона.

(10,43 + 1,59) : (3,29 + 4,26) =  12,02 : 7,55 = 1,592

Получается коэффициент довольно близкий к ”золоту”».

Но высота стилобата от нулевой отметки не 1,59, а 1,887 м (вместе с высотой колонны, взятой с капителью, это 12,317 м), а высота фронтона с антаблементом по нашим расчетам 7,619 м. Исследователь почему-то просто проигнорировал евтентерий – нижнюю ступеньку Храма. Итак:

12,317 : 7,619 = 1,617 → Ф

Радзюкевич, резкий и последовательный противник гипотезы об осмысленном использовании золотого сечения в архитектуре античности и средневековья, в своей диссертации пишет о методологии исследования архитектурных форм, разработанной во второй половине XX в. Джим Коултоном: «Наиболее наглядно метод Дж. Коултона можно продемонстрировать на выявленном им правиле классического периода. По этому правилу размеры стилобата определяются через рядовой шаг колонн».

Но так и утверждал Витрувий, полагавший, что у одного из видов «правильных храмов» диаметр колонны, умноженный на два с четвертью, дает шаг колонн[5].

Применим методику Витрувия к Парфенону. Оказывается, проще всего взять за базовый размер то, что базой и является – ширину стилобата:

Если ее умножить на два с четвертью, то получим длину стилобата. Если ширину стилобата поделить на два с четвертью, то получим высоту ордера.

Если поделим ту же ширину стилобата на 10 ´ Ф, то определим диаметр рядовой колонны 1,908 м. А, умножив диаметр рядовой колонны на два с четвертью, определим шаг рядовых колонн (4,295 м).

Если взять диаметр угловой колонны, равной 4 дл и умножить его на два с четвертью, то получим шаг колонн по длине стилобата.

Выходит, пропорции Парфенона ориентированы на пропорцию 9/4 (то есть два с четвертью) и те, которые мы сегодня называем золотыми. Только пользовались древние мастера, видимо, не иррациональным числом 1,618…, а числом Ф* (т. е. отношением 55/34).

ШКАЛА ЗОЛОТОЙ ЛИНЕЙКИ

Пытаясь целочисленно выразить геометрическое золото, античные геометры должны были действовать простым перебором. Геометрически построив отрезок, древний математик должен был найти величину, кратную его частям.

Предположим, отрезок в три олимпийских фута (0,92613 м) – это диагональ некоего полуквадрата. Геометрически по золотому сечению он делился на два:  0,57238 и 0,35375 м. Вот только, работая циркулем, чисел мы не получим. И линейка с мерной шкалой нас тоже не выручит, поскольку мерной шкалы еще нет, и ее только надлежит разбить.

Первое приближение к золотому сечению дает деление отрезка на 13 модулей (пропорция 8 : 5). Однако 0,567 м  (таковы восемь модулей при делении трех футов на 13 частей) отличны от геометрической длины большего отрезка почти на 2,4 мм.

Ошибка бросается в глаза.

При делении трехфутового отрезка на 21 модуль, отношение 13 к 8 даст погрешность в 0,9 мм, а при 34 модулях получим едва различимое глазом отклонение в 0,4 мм.

И только поделив общий отрезок на 55 частей (по 0,0168 м), математик должен был обнаружить, что в большей части 34 деления (0,57252 м), а в меньшей их 21 (0,35361 м)

Обнаружить отклонение в 0,14 мм даже при тщательном построении нереально.

Уточним размеры Парфенона по золотому сечению.

По А. В. Радзюкевичу высота Парфенона должна быть 40 дл. Жаль только, что с учетом высоты евтентерия (тонкой надземной части лежащей под храмом нижней плиты) это красивое число превращается в 40,6 дл (19,907 м). При этом высота ордера (антаблемент + колонны с капителью) по обмерам – 13,728 м (28 дл).

Но удвоим высоту колонны с капителью (2 ∙ 10,43 м = 20,86 м) и, начиная с этого размера, станем последовательно делить на число Ф* (то есть 55/34):

20,86

: Ф* =

12,895 м (три шага колонны = 12,885 м)

: Ф* =

7,972 м  (фронтон + антаблемент + абак = 7,97 м)

: Ф* =

4,928 м  (фронтон + карниз = 4,923 м)

: Ф* =

3,046 м  (фриз + архитрав + абак = 3,048 м)

: Ф* =

1,883 м  (стереобат с евтентерием = 1,887 м)

: Ф* =

1,164 м  (толщина боковых стен наоса, то есть помещения самого храма = 1,16)

А поделив высоту антаблемента (3,297 м = карниз + фриз + архитрав) на Ф*, получим 2,038 м. Это толщина торцевых стен наоса.

Это говорит о том, что вертикальные размеры Парфенона и впрямь расчислены по золотому сечению. Но в случае с фронтоном и карнизом, а также с членением более мелких деталей (к примеру, капителей) строители пользовались не целочисленным переводом иррациональных величин в целочисленные, а шнуром, позволявшим избежать ошибки перевода. 

Высота стереобата с евтентерием должна была настроить вертикальные пропорции фасада на золото.

Итак, основные пропорции вертикали фасада и впрямь оказываются золотыми.

ЗОЛОТОЕ СЕЧЕНИЕ ПАРФЕНОНА

При этом нужно добавить, что пропорция W/D, то есть три шага колонны к высоте колонны с капителью, дают пропорцию 2/Ф, и если брать по обмерам Баланоса, то отклонение ничтожно (1,2354 вместо 1,2361), а пять шагов колонны к высоте тела колонны дадут 2,24, то есть приближение к √5.

ВЫСОТА КАПИТЕЛИ РЯДОВЫХ КОЛОНН ПАРФЕНОНА

У современных Парфенону дорийских храмов в Пестуме пропорциональная проблема видна невооруженным взглядом: толстые колонны, напоминающие ноги персидских боевых слонов и тяжелый верх. В Парфеноне эта проблема решена с помощью целочисленного приближения к √2, √5 и золотой пропорции. Но, как это ни странно, в пестумских храмах используются те же пропорциональные принципы. И на чертеже все выглядит весьма привлекательно. Однако только на чертеже.

ХРАМ ГЕРЫ В ПЕСТУМЕ. ПРОПОРЦИОНАЛЬНАЯ ПРИКИДКА

Cамо по себе использование иррациональных и трансцендентных констант к гармонии не приводит. То, что может быть красиво на плоскости, при механическом использовании приема (ради самого приема) в объеме зачастую превращается в нечто мертвое и тяжеловесное.

Почему в одних пропорциях гармонические константы вступают в диалог и составляют некое новое парадоксальное единство, а в других рассыпаются, мы пока не знаем. Впрочем, ни золотое сечение, ни другие гармонические константы на фасаде этого храма зрительно не акцентированы.

В любом искусстве стиль – это способ сворачивания пространства. Архитектуру недаром называют застывшей музыкой, ведь в ее объектах свернутым (а потому и почти что отмененным) оказывается время. Потому-то в Гизе и было когда-то сказано, что время боится вечности, а вечность боится пирамид.

продолжение сюжета

к началу сюжета