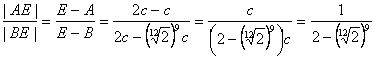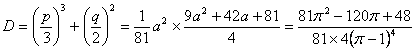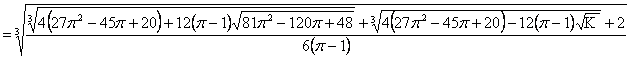Правка и
добавления от 12 апреля 2009
Заметки о вечном.
Продолжение темы «Серебряное
сечение»
http://chernov-trezin.narod.ru/ZS_1_4.htm
π-ОКТАВА (о триадной природе
музыкального строя) СОДЕРЖАНИЕ
СТРАНИЦЫ: – М. Борбат. Уравнение Чернова – А. Чернов. π-октава
и триадная природа музыкального строя – Шкала частот серебряного строя – А. Чернов. Октава
солнечного спектра NB: Читатель, не
склонный к чтению текстов с математическими формулами, может получить
представление о выложенной ниже статье М. В. Борбата из моего письма к
московской певице Д. Б.: Даша,
ты не права, эти формулы, если они верны, как раз для тебя, – для твоего
пения. Объясняю для любимых «теток-идиоток» (цитата из Пелагеи
Марфовны, а на нее обижаться грех): в этих математических выкладках, смею
полагать, содержится то решение проблемы темперации октавы, которое искал, но
не нашел в 550 году до н. э. Пифагор. Он брал от эталонной ноты интервалы по
чистой квинте. И... получил «волчью квинту» да «пифагорову комму» – дурные,
фальшивые интервалы. Выяснилось это почти через два тысячелетия, уже в
средневековье, когда органы в храмах на некоторых аккордах стали истошно
выть. В эпоху Возрождения это исправили равномерной темперацией, немного
передвинув ноты и распределив пифагорову комму по всем 12 интервалам октавы.
Темперация по корню из двойки оказалась на удивление тупой (это как резать
тупым скальпелем), и в результате возникла теория зонного слуха: мол, от
такого-то тона до такого-то есть интервал, в котором нота звучит правильно. Представь, будто вместо числа π, равного 3,14…, до
сих пор пользовались бы «красивым» числом «3». Только колесо, чей диаметр
сделан по одной трети от длины обода, почему-то плохо катится. Начиная с Пифагора,
искали (и до сего дня ищут) компромисс – то колесо делают поменьше, то много
колес разного диаметра нанижут на одну ось. Выдвинули даже теорию, мол,
колесо не может быть круглым, потому что идеально круглого в природе вообще
не существует. Но худо-бедно, шибко-тряско, а телега все-таки катится. Но
вдруг оказывается, что надо отказаться от красивого круглого числа в пользу
круглого колеса… (И что тут начинается!..) Лет двенадцать назад, заметив что классическая малая
терция (ее еще называют минорной) на удивление близка к значению длина витка
октавы минус диаметр витка («серебряное сечение»), я предложил перенастроить
рояль по числу π. Даже толковал об этом с теоретиками из консерватории.
Встретил понимание. Но поставить этот эксперимент в те годы нам не удалось. Я предлагал все ноты справа от ля I октавы
сдвинуть по высоте звучания чуть-чуть вверх, а расположенные слева от того же
ля – вниз. Всё – в пределах принятой настройки. При этом от ноты «до» до ноты
«до» более высокой октавы тон повышается не в 2, а в 2,02 раза. А малая
терция становится основной – она диаметр от витка октавы (по моему
серебряному сечению, то есть по числу π, так и в природе, и в гениальных
творениях человека – об этом довольно много на моем сайте в разных главах
«Ключей от Парфенона»). Программист Михаил Борбат вывел формулу нового полутона
октавы, настроенной на серебряное сечение (π-октавы). Вроде бы выходит,
что нотный строй с множителем полутона не в 1,0595…, а в 1,0596…, позволит
роялю в унисон играть вместе со смычковыми, а певица твоего уровня сможет
петь, не ощущая неловкости от трагического несовпадения с инструментом в
верхних октавах. Петь, не кривя душой и эмоциями. А то вам, певцам, вот уже который век приходится
смирять себя перед всевластием лукаво настроенного инструмента. А.Чернов 7
апреля 2008 ————————————————————————————————————— Михаил Борбат,
программист, Москва УРАВНЕНИЕ ЧЕРНОВА(уточнение музыкального полутона
и уравнение серебряного интервала октавы)
В своей книге «Хроники изнаночного
времени» петербургский исследователь Андрей Чернов ставит вопрос, имеющий, на
наш взгляд, прямое отношение к одной из актуальных проблем современного
музыковедения. Вот что он пишет: «Если
одну октаву (от ноты до и до следующего до) принять за виток
спирали, то малая терция будет соответствовать по частоте ноте ля. Но
в темперированном (классическом) строе отношение 5/6 уже не работает:
камертонное ля равно 440 герцам, а мы по эталонному до II
октавы (523,25 герц) получаем ля I октавы в 436,04 герц. В
XVI столетии октаву разделили на двенадцать равных интервалов. Они рассуждали
так: если от до до до частота ноты удваивается, то
темперированный интервал должен быть 12√2. (Умножив
двенадцать раз число 1,0595..., получаем искомую двойку.) Симфоническая
музыка выросла из темперации октавы. Но,
понимая, что темперированная гамма — виток спирали, музыковеды вот уже три
века не могут уйти от линейных представлений времен позднего Средневековья,
хотя все музыканты слышат, что клавишные инструменты почему-то очень плохо
звучат рядом со смычковыми. Можно
допустить, что на самом деле темперированный полутон не равен 12√2,
но только близок к этому числу[1].
И скрипач, и певец, и человек за роялем — все они настроены природой по числу
π, а не по квадратным корням. Потому-то, надо полагать, опытные
настройщики всегда перестраивают фортепьяно для игры со смычковыми, чуть
повышая (по сравнению с эталонной) частоту каждого следующего до (а на
самом деле – каждой ноты). Отказавшись
от сведения трансцендентной пространственно-временной гармонии к
иррациональной гармонии диагоналей квадратов, мы откажемся от попытки
выразить π через √2. И получим другое решение проблемы темперации
и другое определение малой терции: малая (минорная) терция — это диаметр
частотного интервала от данной ноты до аналогичной ноты более низкой октавы,
то есть серебряное сечение октавы. В этом случае, взяв эталонные значения
до I и II октав, мы получим отклонение от камертонного «ля» только в
0,02 герца. Это значит, что интервал каждой октавы надо расширить
на несколько центов. СПРАВКА: Принято
делить темперированный полутон на 100 частей (центов). При
изучении чувствительности к различению высоты звука был установлен порог – 6
центов, но при экспериментах психологи засвидетельствовали и исключительные
случаи различения – 1-3 цента. Ньютон после опытов по разложению призмой
белого цвета на составляющие разделил цветовую гамму
по соотношениям простейшей фригийской гаммы, заявив, что “...ширина семи
основных цветов спектра пропорциональна семи музыкальным тонам гаммы или семи
интервалам между нотами октавы”. С тех пор мы и пользуемся архаичным по сути
цветовым строем, очень мало соответствующим реальной “музыке сфер” и просто
музыке, а значит, и гармонии вообще». Поясним то, о чём здесь говорится,
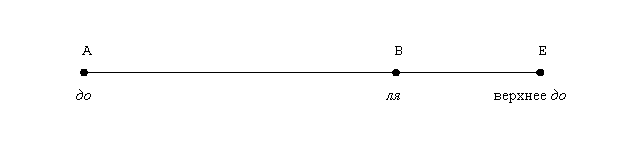
при помощи рисунка.
Интервал AE соответствует
октаве, интервал BE — малой терции. Обозначим через c Гц
значение частоты звука, соответствующего точке A. Тогда (при темперированном строе) точке E будет
соответствовать звук с частотой 2c Гц,
а точке B — звук с частотой (12√2)9c Гц.
Запишем теперь отношение длин отрезков AE и BE:
Замечательное наблюдение Андрея
Чернова состоит в том, что полученное значение (1) крайне (до третьего знака после
запятой) близко к отношению длины окружности к её диаметру, т.е. к числу
π. Далее он предлагает заменить число 12√2, использующееся в темперированном
строе для вычисления полутона, на какое-то другое, чуть большее, так чтобы
отношение (1)
совпало с числом π. Обозначим это искомое число через x. Заметим, что в соответствии со смыслом задачи должно выполняться
неравенство:
В нашем новом музыкальном строе VI ступени будет соответствовать звук
с частотой x9c Гц,
VIII
ступени — звук с
частотой x12c Гц.
Пусть этим звукам соответствуют точки B’ и E’. При этом должно выполняться
равенство (аналог равенства (1)):
Сделаем замену y = x3. Заметим, что из неравенства (2) будет следовать:
Немного преобразовав равенство (3), получим уравнение четвёртой
степени с одним неизвестным:
Решив это уравнение, мы сможем получить
искомое число x. Однако решать его “в лоб” мы не
будем (потому что это слишком сложно), а сначала немного упростим. После ряда
простых преобразований запишем:
В силу неравенства (4) мы можем поделить обе части
уравнения на (y - 1), после чего, раскрыв скобки и
приведя подобные слагаемые, получим новое уравнение, которое мы назвали
уравнением Чернова:
Это — кубическое уравнение с одним
неизвестным. Запишем его канонический вид:
Сделаем замену z = y – a / 3 и запишем приведённое уравнение:
Будем решать его методом Кардано.
Находим дискриминант:
Легко видеть, что дискриминант
больше нуля, следовательно, уравнение имеет одно действительное решение. Оно
находится по формуле Кардано:
Теперь мы, наконец, можем найти
значение числа x:
Посмотрим, каким образом новые
значения полутона и октавы соотносятся с использующимися при темперированном
строе[2].
Таким образом, интуитивное предположение
о том, что октава должна быть расширена на несколько центов, подтверждается.
Количество этих лишних центов читателю предлагается рассчитать
самостоятельно. Список использованной литературы: 1. А. Чернов. Хроники изнаночного времени. СПб, «Вита Нова». 2006. С. 162–163. 2. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся втузов. М., «Наука». 1986. Андрей ЧЕРНОВ π-ОКТАВА И ТРИАДНАЯ ПРИРОДА МУЗЫКАЛЬНОГО СТРОЯ Эту статью утром 1 апреля 2008 года прислал мне молодой
московский программист, а в недалеком прошлом бас-гитарист саратовской группы
«Овертюд», Михаил Вячеславович Борбат. Поначалу я и принял статью за
первоапрельскую шутку: в сочетании с явно стебовым заголовком вид чудовищных
формул выглядел и впрямь комичным. Эдакая жесткая классика жанра. Однако жанр
требовал, чтобы адресат догадался, в чем тут «фишка», а в чем «прикол».
Вооружившись калькулятором, я проверил конечный результат. До седьмого,
последнего в окошке дисплея знака после запятой, число совпало с тем, что для
расширенной по
серебряному сечению октавы я в середине 1990-х
получил на этом же стареньком, подаренном мне старшей дочерью калькуляторе[3].
Получил не по формуле, а хрестоматийным для любого дилетанта «методом тыка». Через пять дней рецензию на работу М. В. Борбата прислал мне
московский математик Алексей Н. Письмо больше напоминало телеграмму: «Андрей,
математическая часть
(преобразование уравнения) вроде бы верна, ну а в нотной грамоте я ни
бум-бум». Два слова о «методе тыка». До того, как М. В. Борбат вывел
формулу[4],
я использовал свой обычный способ поиска серебряного сечения: чтобы
определить его точку, надо от длины окружности вычесть ее диаметр. В случае с музыкальном звукорядом виток октавы надо было чуть
раздвинуть, сохранив при этом высоту эталонного ля I октавы в 440 герц. Но насколько раздвинуть? На калькуляторе не составляло труда подобрать нужный множитель,
который, как оказалось, лишь в четвертом по запятой знаке расходится с коэффициентом
принятого ныне темперированного полутона. Когда высоты нот I (серебряной) октавы
определены, можно предпринять их проверку. Для этого требуется от взятой в
герцах частоты верхней ноты витка отнять частоту такой же ноты, находящейся
на октаву ниже. Это и будет длина витка. Полученный результат надо разделить
на π и получить
диаметр витка. А затем от значения вершины интервала (то есть от значения верхней ноты витка) отнять величину диаметра. Это и
будет точкой серебряного сечения π-минорной терции. В
выведенной М. В. Борбатом формуле π-полутона слышна рифма с квадратным
уравнением, решение которого дает число золотого сечения Ф = 1,618… (Напомню,
что это квадратное уравнение выглядит так: x2
–
x – 1 = 0). Формула серебряного множителя проста:
у = x3 x = 1,0595518… Но, если не бояться больших степеней,
можно записать и так: (π – 1) x9 – x6 – x3 – 1 = 0 Раздели
девять раз частоту ля I октавы на серебряный множитель x3, и получи низ интервала (до I октавы),
умножь три раза ту же частоту на серебряный множитель, – найдешь значение
вершины интервала (до II
октавы). Шаг
равномерно темперированной октавы – двойка, но октава – не круг, а
незамкнутый виток спирали, и потому шаг серебряной π-октавы чуть больше двойки:
Именно
поэтому квадратный корень из двойки может быть лишь неким приближением, более
или менее приемлемой попыткой выразить трансцендентное (по числу π) через иррациональное (по корням из двойки). Повторим:
в случае
серебряного строя длина окружности каждого витка октавы удлиняется
относительно предыдущего не в 2, а в 2,002… раза. Перед
нами расширяющаяся спираль. Условно будем считать, что двойка – величина
расширения витка, а иррациональный хвостик 0,02… – результат вертикального
(если смотреть на спираль сбоку) шага между витками. (В ныне принятом случае
равномерно темперированного клавира получаем не спираль, а серию вложенных
друг в друга и друг с другом не связанных концентрических окружностей.) Взяв
отношение серебряного полутона к равномерно темперированному, получим число
«коэффициента кривизны»: 1,0000837… Во
столько раз «кривое» октавы длиннее «прямого». Около 550 года до н. э. Пифагор предложил свое решение проблемы
звукоряда. Пифагорейцы сделали справедливое наблюдение: если струна
стала вдвое короче, то звук ее будет вдвое выше. Из этого возникло понятие
октавы (как круга) и ее простейшие пропорции: скажем, в натуральном строе октава 1/2, квинта 2/3,
кварта 3/4, большая терция 4/5, малая терция 5/6, большой полный тон 8/9,
малый полный тон 9/10, и диатонический полутон 15/16. В Пифагорейском строе звукоряд создавался путём наложения чистых квинт на
эталонный звук. Но при этом строй все же оказывается незамкнутым: двенадцать
квинт в сумме должны дать семь октав, однако последняя квинта в нем на комму
(примерно четверть полутона) короче других («волчья квинта»). Возникли и
другие чисто музыкальные проблемы: выяснилось,
что пифагорейский строй работает далеко не всегда, и органы в католических
соборах в некоторых позициях начинают фальшивить. СПРАВКА: Темперация (от лат. temperatio — правильное соотношение,
соразмерность) в музыке, выравнивание интервальных отношений между ступенями
звуковысотной системы. Сущность Т. состоит в небольших изменениях величины
интервалов, главным образом квинт, по сравнению с их акустически точной
величиной (по натуральному звукоряду). Эти изменения делают строй замкнутым,
позволяют использовать все тональности и аккорды самой различной структуры,
не нарушая сложившихся эстетических норм восприятия интервалов, не усложняя
конструкции инструментов с фиксированной высотой звуков (типа органа,
клавира, арфы). Потребность в Т. возникла в 16–18 вв. с появлением новых
музыкальных форм и жанров, с развитием средств музыкальной выразительности. В
применявшихся до этого пифагоровом и чистом строях имелись небольшие высотные
различия между энгармоническими звуками: не совпадали по высоте друг с
другом, например, звуки си-диез и до, ре-диез и ми-бемоль. Это тормозило
развитие ладотональной и гармонической систем: нужно было или конструировать
инструменты с несколькими десятками клавиш в октаве, или отказаться от
переходов в далёкие тональности. В первых, неравномерных темперациях
музыканты пытались сохранить величину большой терции такой же, как в чистом
строе. В 12-ступенном
равномерно-темперированном строе все чистые квинты уменьшены на 1/12
пифагоровой коммы; от этого строй стал замкнутым, октава оказалась
разделённой на 12 равных полутонов и все одноимённые интервалы стали
одинаковыми по величине. Психофизиологической основой использования нового
строя явилась открытая позже зонная природа звуковысотного слуха. Попытки
преодолеть интонационные недостатки 12-ступенной Т. путём создания строя с
24, 36, 48, 53 и большим количеством темперированных ступеней в октаве не
увенчались успехом, 12-ступенная Т. остаётся оптимальным решением проблемы
строя. Ю. Н. Рагс. БСЭ. В 1533 году итальянец Джованни Мария
Ланфранко издал в городе Брешия методическое руководство по настройке музыкальных
инструментов «Блеск музыки» («Scintile di musica»). Он разделил октаву разделил на двенадцать равных
интервалов по множителю корня из двойки двенадцатой степени. Вопросом, почему
корень из двойки должен быть связан с длиной окружности, с тех пор не
задавались, ведь найденное решение, хотя и не сразу, но всех устроило[5].
Была
допущена простая логическая ошибка: из того, что поделенная надвое струна
звучит в два раза выше, вовсе не следует, что одноименные ноты смежных октав
по своей частоте должны отличаться ровно в два раза. Вот что пишет
московский настройщик с сорокалетним стажем Александр Александрович
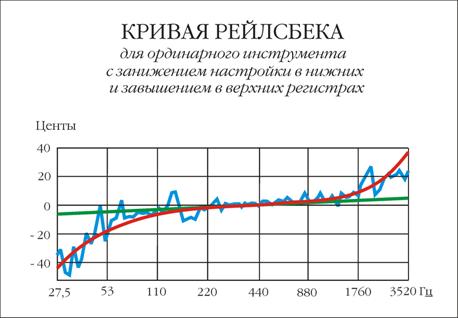
Мельников: Не менее сложна работа с крайними регистрами
фортепиано, которые настраиваются по так называемой «кривой Рейлсбека», когда
для согласования звучания по всему диапазону в нижнем регистре строй
занижается, а в верхнем завышается. Это связано как с психофизиологическими
особенностями восприятия крайних регистров, так и с негармоничностью струн. У
струн помимо основной частоты колебаний есть множество обертонов, которые
активнейшим образом влияют на восприятие высоты. Теоретически эти обертоны
должны располагаться по математическому ряду, но в реальных струнах обертоны
завышены, что очень затрудняет восприятие высоты звучания (особенно в басовом
регистре), и может привести к ошибочному мнению, что настройщик плохо
настроил интервалы. СПРАВКА: Высота тона – субъективно воспринимаемая слухом частота звукового сигнала.
Субъективно воспринимаемую высоту тона называют мелодической и измеряют в
мелах. Зависимость высота тона от его реальной частоты – нелинейна.
Субъективно воспринимаемая человеком высота звука сильно зависит от его
частоты. Этот феномен учитывают при настройке музыкальных инструментов. К
примеру, настройка фортепиано производится с учетом так называемой «кривой
Рейлсбека». Эта кривая вычислена
работавшим в 1937 году на фирме «Стейнвей» американским профессором О. Л.
Рейлсбеком, который при помощи специального электронного прибора замерял
частотный строй только что настроенных роялей[6]. Известно, что
разные музыкальные инструменты дают разную амплитуду графика Рейлсбека, и
опубликованный американским исследователем случай относится к конкретному (и
не самому хорошему) роялю. Основатель первой российской школы настройщиков
фортепиано «Квинта-2» Валерий
Григорьевич Порвенков в электронном письме
сообщил мне, что для разных инструментов диапазон отклонений к самым
басовым низам колеблется от – 3 до – 25 (а порой и до – 60 центов) и на такие
же величины, но в сторону завышения, – к дискантам, а из клавишных минимальные отклонения дают концертные рояли. В своей книге
фортепианный мастер пишет: Для пианино кривая Рейлсбека начинает резко подниматься
в дисканте и опускается в басу, в то время как для роялей, особенно больших концертных, она представляет почти
прямую, несколько наклоненную к абсциссе. Но иногда басовые тоны занижаются,
а дискантовые завышаются на меньшую величину, чем обычно, иногда встречается кривая,
лежащая почти горизонтально. Однако такие исключения составляют 5–10% всех
проверенных инструментов. В хороших роялях настройка близко подходит к слегка
наклоненной прямой… В среднем же полутоновые интервалы по сравнению с
темперированными интервалами имеют тенденцию к расширению от 0 до 0,5 цента в
теноровом регистре и от 0,25 до 2 центов в басовом и дискантовом. В пересчете
на октаву это составляет от 0 до ± 6 центов в середине и от ± 3 до ± 24
центов к краям диапазона… Расширение октав в больших роялях на 3 цента на
каждую октаву означает[7],
что октава уже не имеет точного соотношения частот 2:1. Подсчет показывает,
что в этом случае соотношение немного больше и равно примерно 2,001735:1. В.
Г. Порвенков. Акустика и настройка музыкальных инструментов.
М., 1990. С. 85–106. http://www.kvinta2.pravdinskiy.ru/archive.php?chapter=3 Последнее число
(«для хороших роялей»!) до округленного третьего знака по запятой совпадает с
серебряным множителем октавы (2,002…). А это значит, что уже и в первой
половине XX века мастера,
работавшие «на слух», строили рояли не по равномерной темперации, а по
серебряному сечению. После того, как
экспериментатор Рейлсбек сделал свое открытие, прошло более семи десятилетий.
Однако до сих пор полученные Рейлсбеком сенсационные результаты теоретически
не интерпретированы. Если мы нанесем
на график прямую серебряного строя, то увидим, что с Большой октавы до
Третьей (то есть на протяжении четырех октав) графики практически совпадают,
а отклонение по π-формуле на начало субконтроктавы и конец Пятой октавы равны 6 центам.
Кривая настройки пианино (синим) и
сглаженная ее форма (красным) График по вертикалям ля. Пятая октава
на графике отсутствует Зеленым –
расширение π-октав
(влево и вправо от эталонного ля в 440 Гц) В. Г. Порвенков
оказался прав: теоретически кривая Рейсбека – это
правильная прямая, пересекающая ось абсцисс в точке эталонного ля I октавы. В срединных октавах кривая Рейлсбека задана
равномерным расширением π-октав, а потому серебряная
темперация – та гармоническая норма, на
которую настроено природой человеческое ухо. Однако материальный дефект
реальных струн (их практическая «негармоничность»), и, вероятно, некие
особенности периферии человеческого слуха на периферии усиливают тенденцию
искривления графика. (Это похоже на перцептивное искривление зрительного
образа, о которых в своей «Общей теории перспективы» писал Б. В. Раушенбах.) Начав с ноты ля I октавы, умножая (или деля) на число π-полутона
1,0595518, мы получили частоты нот первой и
второй серебряных октав (напомню, что уточненную малую терцию мы и
назвали серебряным сечением). Далее, умножая (или
деля) значение любой ноты на 2,0020102, получили серебряные значения той же ноты для прочих октав. При этом даже самое
низкое до субконтроктавы (16,2738 Гц) оказалось в пределах ныне принятой
настройки (12,27 вместо 16,35 Гц), но это и есть те 6 центов, которые
считаются нормальной «зоной» для экспертов с абсолютным слухом. (См. ниже
таблицы I и II.) И коли так, то
придется вносить коррективы в ныне принятую теорию «зонного слуха»[8],
утверждающую, что даже человек с абсолютным слухом не способен уловить
различие звучания менее 1–3 центов. (На наш взгляд, эта теория – плод линейной
темперации октавы по корню из двойки.) Утверждают, что
Чайковский просил строить свой рояль «с
розливом»[9], то
есть уходя от равномерной темперации. Сухой и мертвой считал правильную
настройку Скрябин. Вот еще цитата из
музыкального справочника: В основе сочного и живого звучания двенадцатиструнной
гитары, аккордеона, баяна, гармони лежит унисон. В аккордеоне, например, звук
каждой ноты генерируется узлом, содержащим два источника колебаний (язычка),
специально настроенных в разлив – с небольшой (в единицы герц) разницей в
частотах. В двенадцатиструнной гитаре звук извлекается одновременно из пары
струн. Разница в частотах образуется естественным путем из-за невозможности
идеально одинаково настроить струны инструмента. Итак,
если взять интервал между одинаковыми нотами двух смежных октав, то
серебряное сечение обязательно придется на одну из нот между ними. И это
всегда будет минорная терция, скорректированная по числу π. К примеру, интервал от эталонного ля I октавы до ля II октавы даст точку серебряного сечения на фа-диез
II октавы (369,9015 Гц), октава по
ля-диез даст в серебряном сечении соль, по си – соль-диез и т. д. СЕРЕБРЯНОЕ СЕЧЕНИЕ
МУЗЫКАЛЬНОГО СТРОЯ
Кварты
и квинты при этом сохранятся, однако может показаться, что они существуют не
сами по себе, а как случайное сближение,
следствие все того же членения каждого витка по числу π. Но это не так. Недостаток равномерной темперации в
том, что это усреднение внутри одной, линейной симметрии, а мы должны констатировать, что гармоничными
оказываются только те пропорции музыкальных частот, которые можно получить,
приблизившись к ним тремя способами – по простейшим целочисленным
(линейным) отношениям дробей (кварта, квинта, две терции и т. д.), по
темперированному полутону и по числу π.
Первый способ – наиболее простой, но потому и грубый, второй дает равномерную
темперацию и некоторое усреднение результата, и только третий описывает
гармоническую природу музыкального строя. Двуприродность – норма в
материальной вселенной: вспомним хотя бы о том, что фотон света – это
одновременно и частица, и волна. Но то, что мы назвали серебряным сечением, –
третья (и, надо полагать, – базовая) природа такого гармонического явления
как европейский музыкальный строй. Ноты – это некие
пространственно-временные сгустки, пропорциональные перекрестки не только
разных, но и разноприродных пропорций. Естественным зазором между
разноприродными пропорциями (одни из них – простейшие дроби целых натуральных
чисел, другие – иррациональные пропорции двенадцати степеней √2, третьи
– основанные на кривизне трансцендентные пропорции серебряного сечения) и
ограничена зона «правильной» ноты[10]. Другими словами, в основе
музыкальной гармонии лежит математический каламбур «прямого» и «круглого», а
сама она – следствие парадокса и синтеза разноприродного – простейших
целочисленных дробей, √2 и серебряного сечения. ТАБЛИЦА ИНТЕРВАЛЬНЫХ
СБЛИЖЕНИЙ π-полутон по уравнению (π – 1) x9 – x6 – x3 – 1 = 0
Мы предприняли попытку настроить
теоретическую базу темперации, и оказалось, что темперация может быть
одновременно и равномерной, и незамкнутой. Через двадцать пять веков мы
вернулись к идее Пифагора, только вместо чистых квинт стали накладывать на
эталонное ля I октавы уточненные по числу π малые
терции. Теперь дело за настройщиками, музыкантами, теоретиками музыкальной
науки и акустиками. Напомню, что именно по серебряному числу π построены
домонгольские храмы Старой Ладоги[11],
практическая акустика которых, по мнению специалистов, превосходит
теоретические выкладки современной науки. ИЗ ПИСЬМА ВАЛЕРИЯ ПОРВЕНКОВА ОТ 14 АПРЕЛЯ 2008 Автор письма отвечает на мой вопрос: «Правильно
ли я понял, что завышение на 1 цент в каждой октаве справа от Первой и занижение
на цент к басам (что и равно π-октаве) делается интуитивно? Или это
все-таки следствие какого-то метода настройки?» И хотя мы говорим о принципиально разных вещах (я – о теоретической базе европейского музыкального строя, а эксперт и мой оппонент о теоретическом обеспечении практической работы настройщика), привожу здесь целиком эту часть, на мой взгляд, бесценного для будущих теоретических построений письма В. Г. Порвенкова. А. Ч. Расширение
октав, при их точной на слух настройке (по нулям биений, насколько это
возможно) происходит автоматом из-за негармоничности обертонов струн. Физика
этого процесса описана в моей книге. То есть для настройщика никакого
расширения нет, если инструмент – концертный рояль и сам настройщик
профессионал своего дела. В отличие от такого расширения, незаметного на
слух, и определяемого на основании измерений частот основных тонов,
существует расширение интервалов заметное на слух, которое делается
настройщиками сознательно путём добавления долей биений в каждую настраиваемую
октаву, что особенно проявляется в крайних регистрах. Причин этому несколько – индивидуальный вкус
настройщика, предпочтение человеческого уха к расширению мелодических
интервалов (они больше нравятся чуть расширенными), стремление нивелировать
хреновую акустику дискантов, когда при точной октаве верхний звук маскируется
нижним и для музыканта октава становится невыразительной. А так – октаву в
дисканте настройщик чуть расширил, вот она уже и зазвучала. Опытность и
знания настройщика тоже не последнюю роль играют, но это случайный фактор. В
целом можно разделить настройщиков грубо на две группы: одни, опытные
настройщики, которые в основном привыкли иметь дело с полноценными
концертными роялями, ни о каком расширении октав (они-то имеют в виду – заметное
на слух расширение) слышать не хотят. Но им невдомёк, что по частотам
основных тонов и их настройку теоретик, который не умеет настраивать,
однозначно охарактеризует как растянутую. Другие настройщики, слышавшие о
каком-то расширении октав, делают, особенно на низкокачественных пианино,
октавы на слух расширенными, и переходят зачастую за меру вкуса. Большая
часть настройщиков болтаются между двумя этими группами, не понимая даже, что
расширение октав бывает разным, заметным и не заметным на слух. Заслуженный деятель искусств, настройщик Станислав
Александрович Громов, рецензент моей книги, говорил категорично – все октавы
надо настраивать точно на слух. Но другой великий настройщик Георгий
Константинович Богино, с которым я лично был знаком, допускал и не возражал
против определённого слухового расширения октав и всего диапазона фортепиано.
В такой настройке содержатся уже две причины, вызывающие расширение октав:
из-за негармоничности обертонов струн и плюс сознательная слуховая растяжка
октав, повышающая эмоциональность интервалов. В зависимости от соотношения
указанных причин и от вида инструмента мы получаем всё многообразие кривых
Рейлсбека в реальности. Но однозначно сказать, что все инструменты надо
настраивать по одной серебряной пи-кривой, я не могу. Что же можно с моей точки зрения увидеть в Вашей
разработке? Это разработка одной из математических моделей приближенного
описания кривой настройки фортепиано. Модель, она и есть модель. С помощью
метода наименьших квадратов можно составить уравнение, которым можно описать
для конкретного инструмента или группы инструментов очень точно его кривую
Рейлсбека, да вплоть даже до случайных отклонений частот основных тонов, хотя
это уравнение будет уж очень сложным. В своей статье «О точности настройки фортепиано
(факторы, влияющие на настройку, контроль и оценку качества настройки) в
сборнике «Повышение качества и совершенствование производства музыкальных
инструментов» (Сборник научных трудов научно-исследовательского
и конструкторско-технологического института музыкальной промышленности),
Москва, 1983. С. 76–123, я привожу свою математическую модель кривой
настройки в виде тангенсоиды: y = 1/a tg(x+/–x0
) +/– C где: y – отклонение частоты тона в центах для
сглаженной кривой от равномерно темперированных частот; х – угол наклона кривой настройки к
оси частот; 1/а – коэффициент наклона; x0 и С – коэффициенты сдвига по горизонтали и вертикали Коэффициенты легко подобрать для каждой кривой
Рейлсбека с помощью разработанной мной тогда номограммы. Но это тоже
усреднённая математическая модель кривой настройки, которая также не
учитывает случайных отклонений от общей закономерности. Откровенно говоря, и Ваша модель, и моя годятся только
для отражения действительности с той или иной степенью приближения к ней.
Разрабатывать на их основе методы настройки бессмысленно, так как они сами
лишь приближенное описание мира музыки». P. S. Все же позволю себе одно уточнение: строя свою формулу, В. Г. Порвенков решает задачи фортепианной настройки и ведет речь о графике частотных отклонений конкретного инструмента, мы же говорим о реальности нематериальной, теоретической. Если наша формула и будет использована на практике, то область ее применения – настройка электронных инструментов. В своей книге В. Г. Порвенков пишет, что расчёты частот на основе
деления октавы на двенадцать равномерных полутонов впервые были выполнены в
1636–1637 годах французским теоретиком Мареном Мерсенном: «Мир впервые узнал
о фундаментальной константе, не менее знаменитом теперь, чем число π =
3,14, интервальном коэффициенте полутона, с помощью которого основной
интервал октаву можно разделить на 12 одинаковых интервалов и рассчитать
шкалу частот равномерно-темперированного строя: 12√2 = 1,05946309…» М. В. Борбату удалось показать, что «фундаментальная константа» оказалась всего лишь следствием серебряного сечения, неким приближением к функции того же числа π. Еще раз напомню, что из уравнения (π – 1) x9 – x6 – x3 – 1 = 0 следует, что х = 1,0595518… Полагаю, впрочем, что серебряный
строй, являясь одновременно и темперированным, и незамкнутым, способен решить
проблему так называемых «биений» (это когда амплитуды звуков накладываются
друг на друга или входят в противофазу, и это приводит то к неожиданному
усилению, то к затуханию звука). Однако это лишь предположение. 5 апреля–16
июня 2008 P.S. Из письма А. А. Мельникова от 27 мая 2008: Практически
все октавы в фортепиано расширены относительно математического строя (ОСТ
7710), хотя настроены без биений между основной частотой струны и гармониками
октавных струн, что и подтверждает Ваши утверждения. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ТАБЛИЦА I
ШКАЛА
ЧАСТОТ СЕРЕБРЯНОГО СТРОЯ
высота звука в
герцах
серебряный
полутон 1,05955179365421
расширение
октавы 2,00201022913774
|
|
Субконтроктава |
Контр- октава |
Большая октава |
Малая октава |
Первая октава |
Вторая октава |
Третья октава |
Четвертая октава |
Пятая октава |
|
до |
16,27(37556…) |
32,58 |
65,23 |
130,58 |
261,428515843 |
523,38(26) |
1047,82 |
2097,74 |
4199,7 |
|
до-диез |
17,24 |
34,52 |
69,11 |
138,36 |
276,997052874 |
554,55 |
1110,22 |
2222,67 |
4449,8 |
|
ре |
18,27 |
36,58 |
73,23 |
146,6 |
293,492724209 |
587,58 |
1176,33 |
2355,03 |
4714,79 |
|
ре-диез |
19,36 |
38,75 |
77,59 |
155,33 |
310,97074236 |
622,57 |
1246,38 |
2495,27 |
4995,57 |
|
ми |
20,51 |
41,06 |
82,21 |
164,58 |
329,489607842 |
659,64 |
1320,61 |
2643,87 |
5293,06 |
|
фа |
21,73 |
43,51 |
87,1 |
174,38 |
349,11130498 |
698,92 |
1399,25 |
2801,32 |
5608,27 |
|
фа-диез |
23,03 |
46,1 |
92,29 |
184,77 |
369,901509376 |
740,55 |
1482,58 |
2968,14 |
5942,25 |
|
соль |
24,4 |
48,84 |
97,79 |
195,77 |
391,929807735 |
784,65 |
1570,87 |
3144,9 |
6296,13 |
|
соль-диез |
25,85 |
51,75 |
103,61 |
207,43 |
415,26993077 |
831,37 |
1664,42 |
3332,19 |
6671,07 |
|
ля |
27,39 |
54,83 |
109,78 |
219,78 |
440* |
880,88(45) |
1763,54 |
3530,62 |
7068,35 |
|
ля-диез |
29,02 |
58,1 |
116,32 |
232,87 |
466,202789208 |
933,34 |
1868,56 |
3740,88 |
7489,28 |
|
си |
30,75 |
61,56 |
123,24 |
246,74 |
493,966001512 |
988,92 |
1979,84 |
3963,66 |
7935,28(94785…) |
* ля-1 поделила строй из 108 нот в пропорции 57/51, что является хорошим целочисленным приближением к функции Жолтовского √5/2.
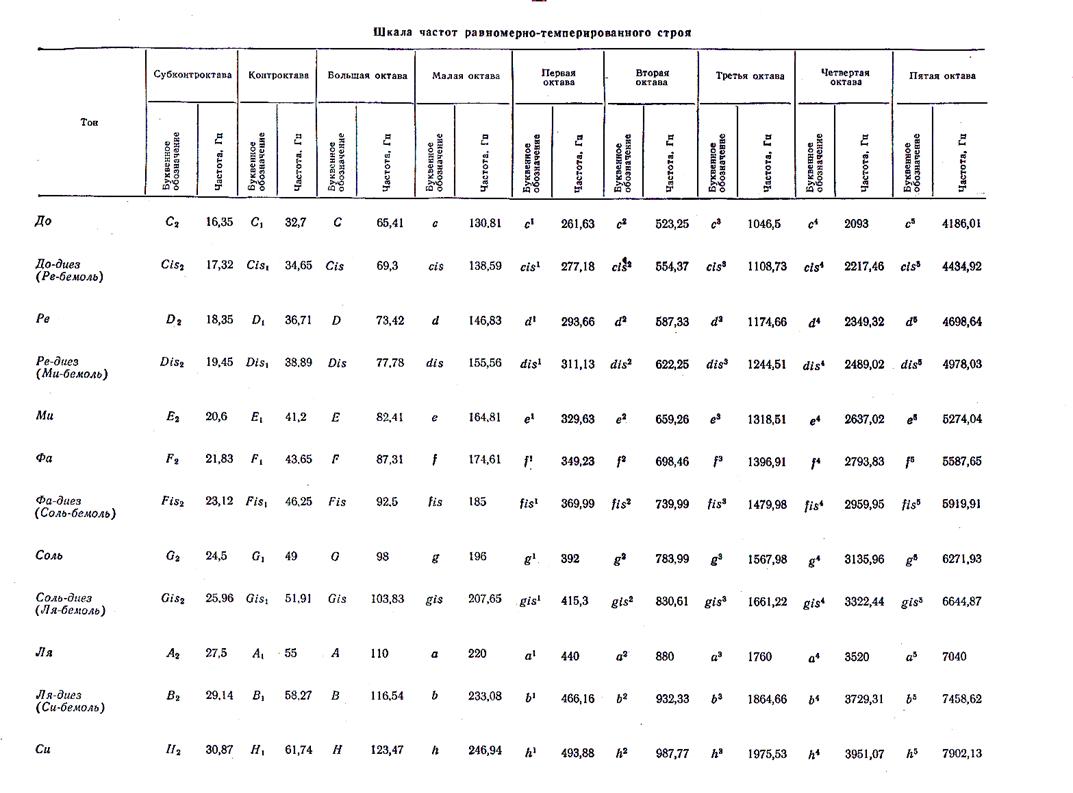
Для
сравнения – таблица равномерно темперированного строя:
ТАБЛИЦА II
Подробнее о серебряном сечении см.:
http://chernov-trezin.narod.ru/ZS_2.htm
|
Андрей ЧЕРНОВ ЦВЕТИК-ДВЕНАДЦАТИЦВЕТИК Покажем,
что семь цветов радуги – такая же культурологическая архаика, как и семь нот
октавы. В школе учат, что существуют основные цвета и
дополнительные. Цвета, которые нельзя получить смешением
красок, – основные. Художники считают, что основных цветов три: красный,
желтый и синий. И так действительно получается, если смешивать те краски,
которыми пишут или рисуют. Однако у физиков иное и весьма категоричное
мнение: основные цвета – красный, зеленый синий. СПРАВКА: Согласно теории Юнга-Гемгольца (1821–1894), ощущение
любого цвета можно получить смешиванием спектрально чистых излучений красного, зеленого и синего. Эта
теория хорошо согласуется с наблюдаемыми фактами и предполагает, что в глазу
есть только три типа светочувствительных приемников. Они отличаются друг от
друга областями спектральной чувствительности. Красный свет воздействует
преимущественно на приемники первого типа, зеленый – второго, синий –
третьего. Сложением излучений таких трех цветов в различных пропорциях можно
получить любую комбинацию возбуждения всех трех типов светочувствительных
элементов, а значит и ощущение любого цвета. Если все рецепторы
возбуждены в одинаковой степени, мы имеем ощущение белого цвета, если
рецепторы не возбуждены – черного. По этой причине, накладывающиеся области красного,
зеленого и синего цвета выглядят как белое пятно. Наложение красного и синего
цвета дает фиолетовый цвет, зеленого и синего – бирюзовый, красного и
зеленого – желтый.
Как это происходит, можно увидеть тут: http://physics.nad.ru/Physics/Cyrillic/rgb_txt.htm Дополнительные (противоположные цвета) по
традиционной семицветной классификации: –
Красный – зеленый. –
Желтый – фиолетовый. –
Синий – оранжевый. Если долго (к примеру, с полминуты) смотреть на
что-то очень красное, а потом перевести глаза на белый лист бумаги, то
увидишь зеленую тень того, на что смотрел. Но если красный с синеватым отливом, то и
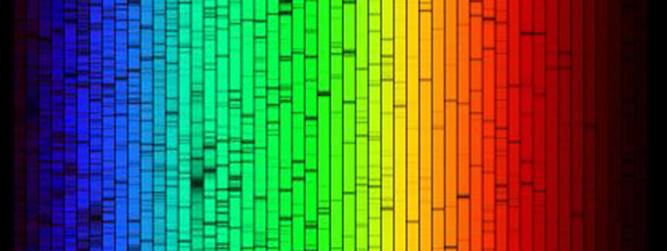
дополнительным будет желто-зеленый. Всё так, однако, не так просто. На
фото солнечный луч, разложенный стеклянной призмой. Широкие полосы красного, зеленого и синего. Почти не просматривается лазоревый и более голубой
его оттенок, который называют бирюзовым – их полосы на стыке зеленого и
голубого слишком узки. Насмотревшись на картинку, превратим ее в негатив и
расположим под первым снимком:
Снимок Найджела
Шарпа. Национальная
обсерватория Китт-Пик. Аппарат – Фурье-спектрометр http://www.astronet.ru/db/msg/1213566 Начальной и очень широкой на негативном изображении
оказалась самая узкая на первоначальном снимке полоса (там она занимает лишь
одну вертикальную колонку шкалы спектрометра). Это полоса лазоревого цвета – негатив
коричнево-сизого и багрово-красного. Но на том же негативе вторая колонка с
противоположного, левого края снимка (сразу вслед за белой) – также
лазоревая. ЧЛЕНЕНИЕ ЦВЕТОВ ВИДИМОГО СПЕКТРА ПО «ВИКИПЕДИИ» (Длина волны в нанометрах) Красный 760–630. Оранжевый 630
(или 620) – 590. Жёлтый 590–565. Зелёный 565–500. Голубо́й (циан)
500–485. Синий 485–440
(или 490–420). Фиолетовый
440–380. Сегодня
принято делить видимый участок солнечного спектра на 12 секторов, а его зона
на шкале электромагнитных колебаний приблизительно от 360 до 760 (иногда
называют и 780) нанометров (эта
единица – длина волны в 1/1 000 000 000 часть метра). Понятно, что перед
нами такой же самостоятельный виток частотной спирали, как и виток октавы, а
множитель его двенадцати ступеней будет равен серебряному полутону 1,0595518…
(либо близок к этому числу). 380–760 (с хвостиком) нм – видимая октава солнечного
света. Ультрафиолетовая область оптического излучения лежит
в пределах 12–380 нм. Это пять невидимых человеческим глазом витков
спектральных октав. Хотя монохроматические излучения с длиной волны
более 700 нм и менее 400 нм уже плохо воспринимаются
человеком со средним зрением, расположим спектральную гамму по витку спирали,
уравняв при этом ширину полос.
ЦВЕТА
ПО ИНТЕРВАЛАМ СПЕКТРА: КРАСНАЯ ГРУППА: 12–1. Бордовый. 1–2.
Багровый. 2–3. Красный. 3–4. Алый. ЖЕЛТО-ЗЕЛЕНАЯ ГРУППА: 4–5. Оранжевый.
5–6. Желтый. 6–7. Зеленый. 7–8. Лазоревый. СИНЯЯ ГРУППА: 8–9. Голубой. 9–10.
Синий. 10–11. Фиолетовый. 11–12. Пурпурно-сизый, переходящий в
черный. При двенадцатицветье образуются три группы по четыре
родственных цвета в каждой: в первую группу (красную) входят цвета с
бордового (коричнево-сизого),
названного так по цвету вина из провинции Бордо, до алого, во вторую
(желто-зеленую) – от оранжевого до лазоревого, в третью (синюю) – от голубого
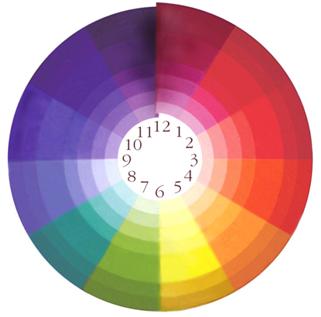
до практически черного. На цветовом круге основные цвета
образуют правильный треугольник. Чтобы найти
дополнительный цвет, надо от нужного цвета провести через центр круга прямую.
При таком делении желтому действительно противостоит
(и дополняет его по принципу перевертыша цветового эха) наиболее темный
диапазон фиолетового[12] –
пурпурно-сизо-черный, а эхо среднебагрового – не зеленый, а лазоревый. Лазоревый цвет в природе столь же редок, как
сказочный лазоревый цветок. Не часто встречается он и в полиграфии (одно из
немногих исключений – марка фирмы «Сименс»). Дело в том, что лазоревый плохо
воспроизводится полиграфическими средствами, он не попадает даже в шкалу
предназначенных для начального художественного обучения «цветовых кругов». Границы
цветов условны. Если призмой разложить видимый свет и из белого получить всю
гамму спектра, то можно определить лишь зону, цветоперехода. (На приведенной
выше картинке мы для наглядности обострили цветовые границы, сделав их более
контрастными.) СПРАВКА: Дневной и сумеречный свет воспринимаются
различными рецепторами глаза (палочками при сумеречном свете и колбочками при
дневном свете). При этом палочки обеспечивают чёрно-белое зрение и обладают
очень высокой чувствительностью. Колбочки же позволяют человеку различать
цвета, но их чувствительность гораздо ниже. В темноте работают только палочки
– именно поэтому ночью воспринимаемое изображение серое. Лазоревая граница голубого и зеленого 500 нм. Но если максимальная
чувствительность глаза днем достигается на длине волны 555 нм, то на длину
волны 510 нм она приходится при сумеречном свете. Это цвет морской толщи на
мелководье, однако не в сумерках, а солнечным днем (не потому ли мы говорим
«лазурная волна», что волна не синяя, а лазоревая?). А поскольку в морской
глубине и днем сумерки, логично предположить, что именно таким, черно-белым
зрением с максимумом на 500–525 нм
сотни миллионов лет назад обладал еще не выбравшийся на сушу наш кистеперый
предок. А если так, то зеленый цвет мелководья, – цвет среды обитания
дальнего предка по прямой эволюционной линии всех земноводных, птиц и
млекопитающих. Световой поток натриевой лампы состоит
из излучений на 589 нм и 589,6 нм. Это зона встречи оранжевого и желтого. Человек же лучше
всего воспринимает зелено-желтый цвет, т. е. излучение с длиной волны,
равной 555 нм. Это идеальная
для глаза человека и роста растений длина цветовой волны. В 1977 году
Международный комитет мер и весов подтвердил, что эта длина волны с
частотой излучения в 540·1012 Гц обладает наибольшей
световой эффективностью. Величина в
555 нм соотносится с вершиной визуального
интервала солнечной октавы по √2. Пройдя от этой величины вверх и вниз
шагом серебряного полутона (1,0595518…), обнаружим, что получаем те же
значения, что и в витке I октавы музыкального строя. Но только не в герцах, а
в нанометрах (это просто совпадение, поскольку мы умножаем и делим на
серебряный полутон два очень близких числа). ОКТАВА МУЗЫКАЛЬНОГО СТРОЯ И ОКТАВА ВИДИМОГО СОЛНЕЧНОГО СВЕТА
В академической среде бытует такое присловье:
«Усложнять – просто. Упрощать – сложно». Но залог любого корректного
упрощения – расширение рамок научной парадигмы. Предположу, что на любом
витке частотной спирали мы должны обнаружить двенадцатичастное «октавное»
членение, а, значит, и π-полутон, и серебряное сечение минорной терции. Однако прежде надо уточнить границы дополнительных
цветов, начиная с центра лазоревого (самой тонкой полоски в видимом спектре).
Мы пользовались доступными интернет-материалами и определяли камертон
лазоревого на глаз, не учитывая возможного смещения цветов. Поэтому до того,
как будет поставлен эксперимент со спектроскопом и сделаны новые замеры
частот кругового спектра, эту заметку следует считать сугубо предварительным
сообщением. Литература: Сивухин Д.
В. Общий курс физики. Оптика, М.,
«Наука», 1980 С..132–144 Яворский Б. М., Пинский А. А. Основы физики. Том 2. Колебания и волны. Квантовая физика М., «Наука», 1981 Резников К. М. Цвета
здоровья. Воронежская государственная медицинская академия им. Н.Н. Бурденко.
Прикладные информационные аспекты медицины. Т 4. № 1.
http://www.vsma.ac.ru/publ/vestnik/archiv/priam/V_4_1/PART_1.HTML Прядко
А. Система световых величин.
Журнала «625». 2004. http://rus.625-net.ru/625/2004/03/light.htm апрель–июнь
2008 |
P. S.
Всех, кому интересна эта тема,
прошу
писать мне через гостевую книгу или по почте (см. на титуле
сайта)
Просьба указать тему «Серебряное сечение» (чтоб не потонуло в спаме).