Андрей Чернов. Заметки о вечном

SECTIO AUREA[1]. ИМЯ, ДАННОЕ ПО ОШИБКЕ

всё о золотом сечении

Числа правят миром.

Пифагор

Числа не управляют миром,

но показывают, как управляется мир.

Гёте

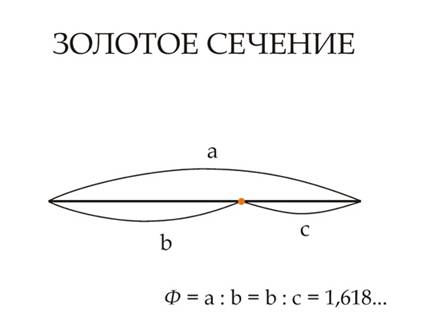
Пойдем к неизвестному от известного, а путь начнем прямо с середины. Только не простой, а золотой.

Золотое сечение («Божественная пропорция», если верить теоретикам времен Возрождения), – пожалуй, самый знаменитый из математических феноменов. Но заговори о золотой пропорции с математиком, и он посмотрит на тебя как на изобретателя вечного двигателя, охотника за НЛО или снежным человеком. Ну а как еще относиться к тому, кто и в XXI веке ищет философский камень, обращающий простой металл в золото?

Для математика в золотом сечении ни тайны, ни загадки: всего лишь решение простенького квадратного уравнения

x²  –  x – 1 = 0

А можно и проще: золотое сечение – среднеарифметическое √5 и 1.

 √5 + 1

 –––––  = Ф = 1, 618…

  2

Однако при этом

√5 – 1         1

 –––––  = –––– = 0,618…

  2            Ф

Золотое число и обратное ему отличаются на единицу. Так что основных золотых чисел, строго говоря, – два: Ф и 1/Ф: умножая на Ф, или деля на 1/Ф, получишь один и тот же результат.

Но математик не для того грыз гранит науки, чтобы тешиться нехитрыми перевертышами, или ломать зубы о философский камень, даже если это камень гармонии.

Для него золотое сечение – ни два, ни полтора.

А оно и впрямь 1,6180339887498948482045868...

Первое упоминание о принципе золотого сечения находим в «Началах» Евклида.

Около 400 г. до н. э. великий александрийский геометр записал удивительное наблюдение:

При среднепропорциональном делении отрезка относительно его краев весь отрезок относится к бóльшей своей части, как бóльшая к меньшей.

Речь о делении отрезка относительно его центра и краев. В общеупотребимом переводе на условный русский – деление отрезка в среднем и крайнем отношении.

Итак, золотая пропорция – точка геометрического равновесия в отношении и целого с его частями, и самих частей. А, следовательно, и некая константа, идеальная для развития объекта, системы или процесса.

СПРАВКА:

О золотом делении упоминает Платон (около 360 года до н. э.). Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора. В частности, есть здесь и такое рассуждение:

«Два члена сами по себе не могут быть хорошо сопряжены без третьего, ибо необходимо, чтобы между одним и другим родилась некая объединяющая с их связь. Прекраснейшая же из связей такая, которая в наибольшей степени единит себя и связуемое, и задачу эту наилучшим образом выполняет пропорция, ибо, когда из трех чисел – как кубических, так и квадратных – при любом среднем числе первое так относится к среднему, как среднее к последнему, и соответственно последнее к среднему, как среднее к первому, тогда при перемещении средних чисел на первое и последнее место, а последнего и первого, напротив, на средние места выяснится, что отношение необходимо остается прежним, а коль скоро это так, значит, все эти числа образуют между собой единство».

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида (около 300 г. до н. э.), где оно применяется для построения правильного пятиугольника. Однако термин «золотое сечение» (goldener Schnitt) введён лишь в 1835 году немецким математиком и Мартином Омом[2] (1792–1872). (Он был младшим братом знаменитого физика Георгия Ома.) Термин появился во втором издании учебника Мартина Ома. В 1854 году в капитальном исследовании о пропорциях человеческого тела тем же термином воспользовался физиолог Адольф Цейзинг[3]. Символ φ (греческая буква “phi”) для обозначения золотого числа 1,618… впервые использовал в начале XX века американский математик Марк Барр. Сделано это было в память и честь античного скульптора Фидия, под чьим руководством возводился Парфенон.

И хотя считается, что Леонардо да Винчи делал иллюстрации к трактату Луки Пачоли «Божественная пропорция» (это как раз о золотом сечении), упоминаний об использовании им золотого сечения не обнаружено.

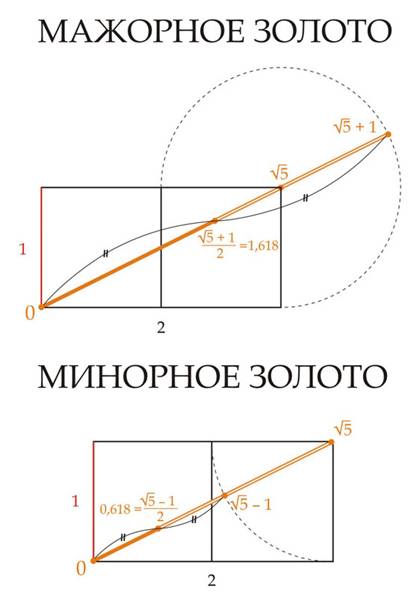
У золотой пропорции две формулы и два числа – мажорное (Ф) и обратное первому[4] – минорное (Ф₁):

Ф = (√5 + 1) : 2 = 1,618...

Ф₁ = 1 : Ф = (√5 – 1) : 2 = 0,618...

И если Ф – решение квадратного уравнение x²  –  x – 1 = 0,

то Ф₁ – решение уравнения x²  +  x – 1 = 0.

Умножая на число мажорного золота (Ф), или деля на минорное золото (1 : Ф), мы получим одинаковый результат. Следовательно, Ф₁ – число, обратное Ф. и При этом не существует других чисел, которые были бы больше своего обратного ровно на единицу. И как мажорное золото на единицу больше минорного, квадрат мажорного золота на единицу больше его самого:

Ф²  = (√5 + 3) : 2 = 2,618...

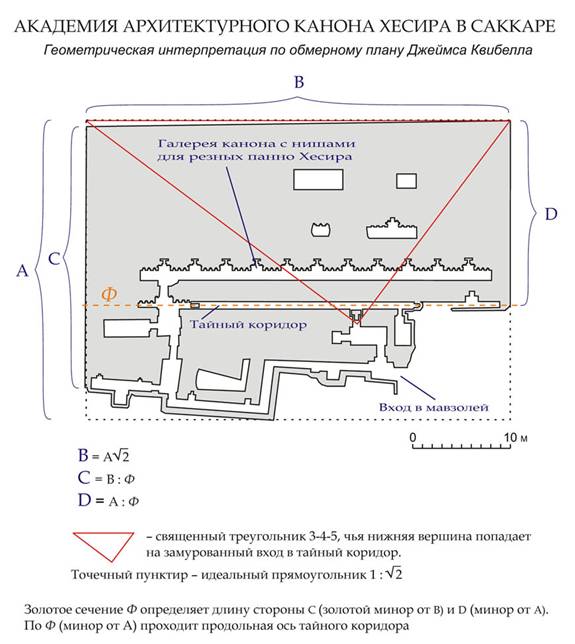
Прогрессия вида 1, Ф, Ф²... Фⁿ – не только геометрическая, это еще и арифметический ряд, в котором каждый его член, начиная с третьего, равен сумме двух предыдущих:

Ф²  = 1 + Ф

Ф³ = Ф² + Ф

Ф⁴ = Ф³ + Ф²

Ф⁵ = Ф⁴ + Ф³

. . . . . . . . . . .

В наши дни феномен золотого сечения окружен плотным и почти непроницаемым для взгляда дилетанта облаком из паранаучных спекуляций, – начиная с мифа о том, что золотой эту пропорцию назвал Леонардо да Винчи, и заканчивая мифическими целебными свойствами построенных по «золоту» пирамид. (Однако это тема для другого разговора и отдельного исследования.)

Математическое и философское изучение «золотых» свойств продолжается уже без малого пять тысячелетий. Древнейший дошедший до наших дней «золотой» древнеегипетский памятник – гробница зодчего Хесира в Саккаре (XXVIII или XXVII век до н. э.), которую можно назвать Академией архитектурного канона, ведь здесь, в нишах галереи стояли деревянные панно с геометрическими иллюстрациями к не дошедшему до нас трактату Имхотепа об архитектуре (сейчас они хранятся в Египетском музее), и, судя по всему, Хесира (Посвященный богу Ра), это – сакральное имя самого строителя первой ступенчатой пирамиды Джосера, легендарного зодчего Имхотепа.

В плане мавзолей Хесира имеет золотую пропорцию (на что, впрочем, до сих пор внимание исследователей не обращалось).

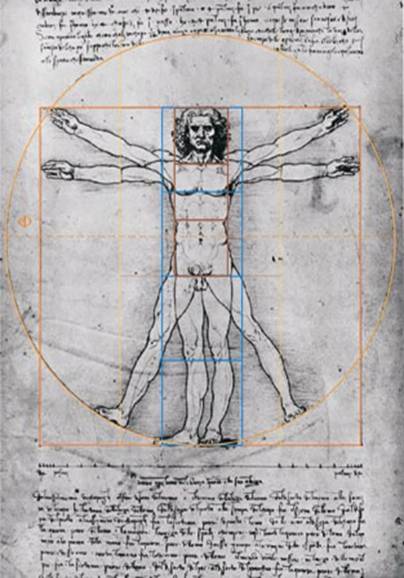
Однако только за последние восемь веков были сделаны несколько фундаментальных открытий, значение и последствия которых, как мне представляется, до сих пор должным образом не осмыслены.

После выхода в 2003 г. романа Дэна Брауна «Код да Винчи» престиж всенародного золотоискательства заметно повысился. Это при том, что русском переводе романа можно прочитать буквально следующее:

– «Все растения, животные и даже человеческие существа наделены физическими пропорциями, приблизительно равными корню от соотношения числа PHI к 1». (Ладно, пусть число Фи недопереведено и названо PHI, но откуда здесь корень, когда речь о самом Ф, то есть о 1,618...?)

– «Семена подсолнечника располагаются по спиралям, против часовой стрелки», а «соотношение диаметра каждой из спиралей к диаметру следующей равно PHI». (Это на сколько же семечки одной спирали должны отстоять от ряда семечек смежной спирали? На самом деле речь должна идти о пропорции числа спиралей, разворачивающихся по часовой стрелке и против нее).

– «Измерьте расстояние от макушки до пола. Затем разделите на свой рост...» и получите, мол, Фи. (Да не Фи, а единицу, поскольку рост – это и есть расстояние от макушки до пола.)

 Виноват не Браун (столь примитивных глупостей в английском тексте нет), а его русский переводчик. Но утверждение о том, «Витрувианский человек» Леонардо да Винчи (знаменитый рисунок Леонардо, где человек вписан в квадрат и круг) назначен иллюстрировать Фи-пропорции человеческого тела, – явно на совести автора оригинала, потому что никаких Фи-пропорций в этом рисунке нет, хотя и это заблуждение и кочует из одного золотого опуса в другой (и той же поддельной пробы).

Поясню: античный теоретик архитектуры Витрувий в начале третей своей книги пишет, что культовые здания должны иметь пропорции человека. И добавляет, что человеческое тело есть модель пропорций, поскольку, если человек раскинет руки и ноги, то фигура вписывается в совершенные геометрические фигуры: квадрат и круг.

Увы, не вписывается. Для этого достаточно (вслед за архитектором Игорем Шмелевым) измерить длину ног от шейки бедра (фактически от тазобедренного сустава) до стопы. И оказывается, что длина раскинутых ног Витрувианского человека короче первой пары его собственных ног почти на 1/10.

То есть, если человеческое тело и вписывается в круг, то до верха этого круга можно достать, только очень сильно подпрыгнув.

В иллюстрации Леонардо к Витрувию золотого сечения нет не потому, что пупок находится на высоте 1,64 (а не 1,62) от роста, а потому, что вся логика построения тела по Витрувию исключает золотую пропорцию. Пупок на рисунке – только центр круга, а в основе чертежа квадрат, и только он. Об этом говорят прямые горизонтальные и вертикальные штрихи, которыми Леонардо разделил руки, ноги, и тело человека: ноги – половина роста, половина от длины ног – их заколенный сгиб. Руки также сгибаются по половине длины (а длина кисти руки – 1/10 от роста).

Само тело, впрочем, поделено на три части (голова с шеей до уровня плечевого сустава; от плечевого сустава до низа ребер; от низа ребер до низа лобка).

Верхнюю точку круга Леонардо получил, прибавив к точке плечевого сустава длину руки. А потом нашел середину и сделал ее пупком.

Витрувианский человек. Рисунок Леонардо да Винчи.

Центр круга – пупок, центр квадрата – низ лобка.

Тело вписано прямоугольник,

короткая сторона которого равна в ¼ большого квадрата.

По вертикали ¼ большого квадрата дает следующие отметки:

низ груди, лобок, сгиб ног.

Пупок не на высоте золотого сечения (Н : 1,62),

а на высоте, полученной из логики членения квадрата (Н : 1,64).

Леонардо не был витрувианцем. Свое графическое рассуждение он предваряет словами: «Витрувий, архитектор, полагает…» И никаких свидетельств о сознательном использовании этим гением Возрождения золотого сечения и даже об интересе его к золотому сечению нет.

СПРАВКА:

В эпоху Возрождения (с конца 14 до середины 16 столетия) художники и ученые пытались объяснить и описать красоту в более научных терминах. Альбрехт Дюрер пытался применить математические принципы к построению идеальной женской фигуры. В результате получилась непропорциональная и совсем не красивая фигура. Тогда Дюрер в своих попытках описания красоты обратился к природе и написал четыре книги о пропорциях человеческого тела. В конце концов, Дюрер пришел к заключению, что там, где речь идет о формах, на Земле нет никого, кто мог бы судить о том, что такое абсолютно самое прекрасное.

ЕЩЕ СПРАВКА:

Альбрехт Дюрер ( Albrecht Durer ). Теоретик искусства. Автор трудов: «Руководство к измерению с помощью циркуля и линейки» (Нюрнберг, 1525); «Четыре книги о пропорциях человека» (Нюрнберг, 1528).

Классик немецкого Возрождения, Альбрехт Дюрер (1471-1528) работая над гравюрой "Немезида или Большая Фортуна" (Ок. 1501) применил принципы пропорционирования Витрувия. Согласно исследованию Эрвина Панофского (1892-1968), признанного корифея европейского искусствоведения, в изображённой фигуре даже размер большого пальца согласуется с Витрувием. Но результат оказался очень далёк от классического идеала и не производил желаемого впечатления, в том числе и на самого Дюрера. В дальнейшем своём творчестве Альбрехт Дюрер от услуг Витрувия отказался, но им самим был написан трактат альтернативный труду Витрувия, полное название которого звучит так: "Здесь заключены четыре книги о пропорциях человеческого тела, найденных и описанных Альбрехтом Дюрером из Нюрнберга на пользу всем любящим таковую науку". В начале трактата Дюрер, критически осмысливший наследие Витрувия, заявляет: "…только совсем слабый разум не верит, что он может найти нечто новое, но держится всегда старого пути, следуя за другими и никогда не осмеливаясь самостоятельно думать". Дерзость у Дюрера сочетается со скромною, о которой он напоминает людям говоря: "Нет также на земле человека, который мог бы окончательно сказать, какою должна быть прекраснейшая человеческая фигура. Никто не знает этого, кроме одного Бога".

Дюрер потерпел поражение: попытка реконструировать человеческую фигуру с помощью математики не удалась.

Большинство золотоносных мифов связано с тем, что названо пирамидоманией (этим заболеванием, как полагает директор Каирского музея и главный хранитель всех египетских древностей доктор Захи Хавасс, обычно страдают пирамидиоты).

В интернете можно найти множество утверждений типа «Пирамида с пропорциями золотого сечения – это генератор жизни и средство гармонизации нашей Среды Обитания». Вот и строители российских «золотых пирамид» (не финансовых, а вполне материальных – из бетона и алюминия) объявили, что вблизи их детищ затягиваются озоновые дыры и снижается уровень правонарушений, а вес предметов изменяется в два раза.

Фригийского царя Мидаса Дионис наградил роковым даром: к чему бы царь ни прикасался, все обращалось в золото. (По другому варианту предания Аполлон одарил Мидаса ослиными ушами.) Все, к чему прикасаются потомки Мидаса, с помощью тех или иных математических преобразований обращается в пропорциональное золото. И сегодняшняя золотая лихорадка уже напоминает ту, что описана Алексеем Толстым в «Гиперболоиде инженера Гарина»: если золота больше, чем грязи, то оно само обращается в грязь.

Почему же тогда и сегодня отнюдь не все математики относятся к этому золоту, как к грязи?

Что бы ни утверждали скептики (см. статьи А. В. Радзюкевича, Е. Г. Назимко, В. С. Белянина на сайте новосибирских архтитекторов[5]), мы можем показать, что исследование и осознанное использование золотой пропорции продолжается уже несколько тысячелетий, и извлеченную из √5 гармонию прямых отрезков в XXVIII веке до н. э. изучал еще строитель первой большой египетской пирамиды зодчий Хесира. Впрочем, разговор о египетских пирамидах, Парфеноне и древнерусских храмах у нас впереди (см. 2–4 главы этой книжки), а потому не будем комкать сюжет беглым пересказом.

Говоря об использовании золотого сечения в античности, первым делом обычно ссылаются на то, что возведенный Поликтетом-младшим амфитеатр в Эпидавре вмещал 15 тысяч человек. В первом ярусе было 34 ряда, во втором 21 ряд (34 : 21 = 1,62). А театральное пространство (окружность основания амфитеатра) поделено в отношении 222,5° к 137,5° (1,618...). Современный исследователь утверждает, что это соотношение углов реализовано в большинстве античных театров[6]. Но брать это на веру это утверждение не стоит: нужны реальные обмеры и конкретные чертежи, а они, увы, не всегда доступны даже специалисту.

Сегодня золотое сечение находят в многообразии природных форм[7], в архитектуре, живописи и музыке[8], в творениях словесности[9]. О нем написаны тысячи работ (пусть и разного достоинства). Тем более странно, что золотое сечение все равно остается загадкой – вроде как перо из хвоста Жар-птицы в руках Дурака.

Горит несамоварным огнем, переливается всеми цветами радуги...

Но где же сама птица?

Известно, что построить пропорцию золотого сечения можно с помощью линейки и циркуля. Разделим квадрат по горизонтали пополам. Проведем диагональ полуквадрата и, приняв ее за радиус, перенесем на вертикаль. Полученный прямоугольник будет прямоугольником золотого сечения

В прямоугольнике со сторонами 1 и 2 (его называют или полуквадратом, или двойным квадратом) диагональ равна √5. Если к этой величине прибавить единицу и полученный отрезок разделить пополам, то мы получим мажорное золото. Если же единицу отнять и остаток разделить на два, то золото будет минорным.

При этом надо помнить, что:

Части относятся друг к другу по удвоенному минорному золоту, когда они получены путем разделения целого на √5.

В эпоху Возрождения золотое сечение именовали «Божественной пропорцией» (Section Divine). Принято за установленный факт, что золотым сечением (Sectio aurea) эту пропорцию» назвал Леонардо да Винчи. При этом ссылаются на изданный в Венеции в 1509 г. трактат Луки Пачоли, посвященный свойствам плоских и пространственных фигур. Но этот труд основателя начертательной геометрии называется «De Divina Proportione» («О божественной пропорции»), и ни о каком «золоте» в нем не говорится.  Иллюстрации к сочинению Пачоли, как полагают (и, вероятно, справедливо, поскольку есть свидетельство самого Пачоли), делал Леонардо да Винчи. Но собственных высказываний Леонардо на данную тему мы не знаем, что бы ни декларировал по этому поводу современный белорусский философ Эдуард Сороко[10].

Считают доказанным, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения (в частности, их находят и «Тайной вечере», «Джоконде»). Но тут сторонники золотого сечения противоречат сами себе: если оно и впрямь – универсальный закон, то наличие его в некоем творении человеческого гения вовсе не свидетельствует о сознательном его использовании.

Термин «золотое сечение» появился лишь в 1835 году. Скорее всего, это просто ошибка памяти Мартина Ома, неточное цитирование им цветистой формулы Иоганна Кеплера (1571–1630), который писал: «У геометрии два сокровища: одно – теорема Пифагора, другое – деление отрезка в  среднепропорциональном отношении. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем».

По Кеплеру золотая пропорция должна бы называться изумрудной или сапфировой. Но поскольку самый драгоценный из камней, конечно, – философский, слов «драгоценный камень» и «мера золота» оказалось достаточным, чтобы через три столетия воспетое Кеплером сечение вполне алхимическим образом обратилось в золотое.

Лука Пачоли утверждал: «...наша пропорция  не может быть выражена ни доступным нам числом, ни какой бы то ни было рациональной величиной и остается скрытой и тайной и поэтому математиками названа иррациональной».

Из этого делают вывод, что итальянский математик нашел лишь некое приближение к золотой пропорции.

Но это ошибка.

ЗАМЕТКИ НА ПОЛЯХ

Пачоли предлагал такие формулы:

I

√125 – 5

–––––––

15 – √125

II

√180 – 6

––––––––

18 – √180

Но можно было бы обойтись и вариантом с подставленными под радикалы двузначными числами:

√20 – 2

–––––––

6 – √20

Ведь все это сводятся к записи:

√5 – 1

–––––

3 – √5

А, домножив числитель и знаменатель на (√5 + 1) : (√5 – 1), получим классическую запись золотого сечения:

 √5 + 1

  ––––– = 1,618...

      2

Лука Пачоли, видимо, не мог не понимать, к чему сводятся предложенные им равенства. Зачем же он скрыл базовую формулу и ввел потомков в искус высокомерного отношения к собственной персоне? Вряд ли найдем другое объяснение, кроме того, что De Divina Proportione для итальянского математика и впрямь была Божественной, и, потому, надо думать, на ее формулу распространялось правило не поминать имя Господа всуе. Пачоли писал: «...подобно тому, как Бог не может быть ни определен, ни словом разъяснен, наша пропорция не может быть выражена ни доступным нам числом, ни какой бы то ни было рациональной величиной и остается скрытой и тайной и поэтому математиками названа иррациональной».

Пачоли полагал, что Божественная пропорция символизирует Троицу (Бог Отец – целый отрезок, Сын – бóльший, Дух – меньший). И смиренно оставлял следующим за ним право самостоятельно сделать столь, казалось бы, легкий и естественный шаг и самим прийти к открытию той Тайны, которая так потрясла все его существо и к которой он подвел своего читателя практически вплотную.

Первые работы, специально посвященные золотому сечению, вышли в конце XVIII столетия. А в середине  XIX века немецкий профессор издал Адольф Цейзинг капитальное «Новое учение о пропорциях тела человека, из остающихся до сих пор непознанных морфологических основ, пронизывающих всю природу и искусство»[11]. В 1855 г. труд Цейзинга был переиздан под названием «Эстетические исследования».

Цейзинг считал, что все в мире можно объяснить золотой пропорцией и рассматривал ее в качестве основного морфологического закона природы и искусства. Он сам сделал тысячи обмеров и показал, что этот закон работает и в пропорциях тела человека и в телах «красивых животных». Немецкий физиолог Густав Фехнер попытался обосновать выводы Цейзинга и обнаружил связь психофизических особенностей восприятия человека и «золотыми» формами вещей[12]. Процитирую из работы Евгения Скляревского: «Фехнер измерил отношения сторон у тысяч окон, картинных рам, игральных карт, книг и других прямоугольных предметов, проверил, в каком отношении поперечные перекладины могильных крестов на кладбищах делят вертикальные основания, и обнаружил, что в большинстве случаев полученные им числа мало отличаются от золотых пропорций. Фехнер разработал целый ряд остроумных тестов, в которых испытываемому предлагалось выбрать «милый его сердцу» прямоугольник из большого набора прямоугольников с различными соотношениями сторон, нарисовать самый «приятный» многоугольник, выбрать место перекладины и т.д. Многократно проведенные опыты показали, что испытуемые отдают предпочтение отношениям, близким к Ф».

В 1958 г. в Англии по методу Фехнера был поставлен опыт: из набора прямоугольников испытуемым предлагалось выбрать те, которые они сочтут самыми красивыми. И большинство (35%) указали на золотой прямоугольник, со сторонами 34:21. (Интересно, что тот же опыт, дал совершенно иные результаты в детской аудитории, из чего делается вывод, что у ребенка совсем иные представление о красивом и гармоничном.)

Выражение «золотая середина» – это не о середине, а о золотой пропорции.

Американец Марк Барр, век назад предложивший обозначать число 1,618… греческой буквой Фи, попал в яблочко. (В XXI веке говорим Фидий – подразумеваем Фибоначчи.) В первой половине XX века, изучая числа Фибоначчи, к неожиданным открытиям приходят голландский математик Абрахам Витгоф, автор теории «игры Витгофа», впервые описанной им в 1905 г., и бельгийскй математик Эдуард Цекендорф. В 1939 г. Цекендорф опубликовал статью, в которой доказал теорему о том, что каждое положительное целое число имеет единственное представление в виде суммы чисел Фибоначчи, в которой два соседних числа Фибоначчи не используются (пример: 30 = 21 + 8 + 1).

В 1957 г. двенадцатилетний (так! – А. Ч.) американский математик Джордж Бергман в журнале «Mathematics Magazine» опубликовал статью «Система счисления с иррациональны основанием»[13], в которой предложил в качестве основания системы счисления использовать золотое число 1,618.... Поскольку, возведенная в степень n, золотая пропорция может быть выражена в виде суммы двух предыдущих степеней, то система Бергмана позволяет делать коррекцию ошибок в аналого-цифровых преобразователях и приводит самосинхронизация кодовых последовательностей при передаче сигнала по каналу связи. (Ныне вчерашний вундеркинд – маститый профессор кафедры математики в Калифорнийском университете, автор двух математических книг, написанных, впрочем, в соавторстве.)

В 1963 г. по инициативе американского математика Вернера Хоггата  и ученого монаха Альфреда Бруссау в США была создана математическая Фибоначчи-Ассоциация («The Fibonacci Quarterly»), которая ежеквартально издает математический журнал The Fibonacci Quarterly. В 1969 г. издательство «Houghton Mifflin» выпустило книгу Вернера Хоггата «Числа Фибоначчм и Люка» (Fibonacci and Lucas Numbers»[14]. А Бруссау был не только монахом, но и фанатичным фотографом: он оставил человечеству снимки двадцати тысяч дикорастущих растений Калифорнии.

В 1969 г., опираясь теорему Цекендорфа, работы американского математика Джулии Робинзон  и еще одну теорему, доказанную в 1942 г. советским математиком Николаем Воробьевым[15], двадцатидвухлетний студент матмеха Ленинградского университета Юрий Матиясевич нашел решение знаменитой в среде математиков 10-й проблемы Гильберта (задача о разрешении Диафантовых уравнений).

В последней трети XX столетия идеи Бергмана и Брусенцова развивает завкафедрой информатики Винницкого государственного аграрного университета А. П. Стахов (с 2004 г. живет в Канаде)[16].

В 1990 г. сотрудником фирмы IBM французский исследователь Жан Перез (Jean-Claude Perez) открыл математический закон, управляющий самоорганизацией оснований Т, С, А, G внутри ДНК. Он обнаружил, что последовательные множества нуклеотидов ДНК представляет собой пропорцию, обеспечивающую разделение ДНК в соответствии с числами Фибоначчи.

Исследователь назвал это «ДНК SUPRA-кодом». А. П. Стахов пишет по этому поводу:

«Рассмотрим любой отрезок генетического кода, состоящий из базисов типа Т, С, А, G, и пусть длина этого отрезка равна числу Фибоначчи, например, 144. Если число оснований типа Т в рассматриваемом отрезке ДНК равно 55 (число Фибоначчи) и суммарное число оснований типа А, С и G равно 89 (число Фибоначчи), то рассматриваемый отрезок генетического кода образует резонанс, то есть, резонанс есть пропорция между тремя соседними числами Фибоначчи (55-89-144). Открытие состоит в том, что каждая ДНК образует множество резонансов рассмотренного вида, то есть, как правило, отрезки генетического кода длиной, равной числу Фибоначчи F_n, разбиваются золотым сечением на множество оснований типа Т (число которых в рассматриваемом отрезке генетического кода равно F_n-2) и суммарное множество остальных оснований (число которых равно F_n-1). Если произвести систематическое исследование всех возможных «фибоначчиевых» отрезков генетического кода, тогда получим некоторое множество резонансов, называемое SUPRA-кодом ДНК. Начиная с 1990 г., указанная закономерность была многократно проверена и подтверждена многими выдающимися биологами, в частности профессорами Montagnier and Chermann, исследовавшими ДНК вируса СПИДа»[17].

Позволим себе еще одну цитату:

«В настоящее время числа Фибоначчи усиленно изучаются бизнесменами и экономистами. Замечено, что волны, описывающие колебания котировок ценных бумаг, являются огибающими маленьких волн, те, в свою очередь, еще более мелких, а количество мелких колебаний в периоде более крупного соответствует ряду Фибоначчи. Впервые это предложил инженер Ральф Hельсон Эллиотт. После серьезной болезни в начале 1930-х он занялся анализом биржевых цен, особенно индекса Доу-Джонса. После ряда весьма успешных предсказаний Эллиотт опубликовал в 1939 году серию статей в журнале Financial World Magazine. В них впервые была представлена его точка зрения, что движения индекса Доу-Джонса подчиняются определенным ритмам. Согласно Эллиотту, все эти движения следуют тому же закону, что и приливы – за приливом следует отлив, за действием (акцией) следует противодействие (реакция). Эта схема не зависит от времени, поскольку структура рынка, взятого как единое целое, остается неизменной. Он писал: "Любoй человеческой деятельности присущи три отличительных особенности: форма, время и отношение, – и все они подчиняются суммационной последовательности Фибоначчи”. Если вы разберетесь с числами Фибоначчи и волнами Эллиота, то можете разбогатеть, играя на бирже ценных бумаг»[18].

По Эллиоту закон волн – это модель развития и упадка, и соотношения между волнами базируются на числах, полученных из ряда Фибоначчи и, в частности, на золотом сечении.

В книге «Закон природы – секрет Вселенной», вышедшей в 1946 году, Ральф Нельсон Эллиот утверждает, что его теория охватывает не только поведение фондовых индексов, но и более общие законы природы, управляющие деятельностью человеческого общества[19].

Эллиот сводит развитие общества к десятку типов моделей движения («волн»), повторяющихся по форме, но не по времени или амплитуде. Согласно теории Эллиота, движение происходит по «старому доброму принципу» три шага вперед два шага назад и волны разделяются на импульсные (вперед) и корректирующие (назад). Базисной является пятиволновая модель, все остальные могут быть выделены из нее.

Но почему тогда волны Эллиота располагаются где-то на маргинальной периферии экономической науки?  Известно, что «девять из десяти трейдеров отказываются от применения волн Эллиота , утверждая, что он никогда не срабатывает». Подсчитано, что около 65% анализа по волнам Эллиота состоит из столь запутанных правил, что десять аналитиков дадут десять разных прогнозов. Вот и заголовок интернетовской статьи экономиста Константина Царихина звучит на удивление знакомо: «Сеанс волновой магии с ее полным разоблачением».

Царихин пишет:

«Автор настоящей статьи не согрешит против правды, если скажет, что любой аналитик, проработавший на рынке более-менее продолжительное время, может подобрать «на заказ» огромное количество графиков с практически любым волновым рисунком. Практика, таким образом, выносит свой вердикт, который, возможно, и огорчит особо рьяных приверженцев теории Эллиота. Этот вердикт звучит так: частный случай. Лягушка, раздувшаяся до размеров быка, увы, лопнула. Чтобы предсказать будущее надо … Трудно сказать, что для этого надо сделать, но уж точно можно сказать, что разбивать график на волны не надо. Все равно это уведет исследователя в сторону»[20].

Как заметил аналитик «Альфа-банка» Владимир Кравчук: «...оптимизированные технические инструменты, хорошо работающие в прошлом, могут плохо работать или вовсе не работать в будущем».

К продолжению сюжета