|
Андрей Чернов. Заметки о вечном. SECTIO AUREA. ИМЯ, ДАННОЕ ПО ОШИБКЕ (2) ЗОЛОТОЕ СЕЧЕНИЕ В ИЗОБРАЗИТЕЛЬНОМ
ИСКУССТВЕ И АРХИТЕКТУРЕ Искусствоведы дружно утверждают, что на живописном полотне существуют четыре точки повышенного внимания. Располагаются они по углам четырехугольника, и зависят от пропорций подрамника. Считается, что какими бы ни были масштабы и размеры холста, все четыре точки обусловлены золотым сечением. Все четыре точки (их называют зрительными центрами) расположены на расстоянии 3/8 и 5/8 от краев (на рисунках в этой книжке золотые точки выделены оранжевым цветом). Полагают, что это матрица композиции любого произведения изобразительного искусства. Вот, к примеру, поступившая в 1785 г. в Государственный Эрмитаж из Академии наук камея «Суд Париса». (Она украшает кубок Петра I.) Итальянские камнерезы не раз повторяли этот сюжет на камеях, инталиях и резных раковинах. В каталоге можно прочитать, что изобразительным прототипом послужила гравюра Маркантонио Раймонди по утраченному произведению Рафаэля. И действительно, одна из четырех точек золотого сечения приходится на золотое яблоко в руке Париса. А если точнее, то на точку соединения яблока с ладонью. Предположим, Раймонди сознательно высчитывал эту точку. Но вряд ли можно поверить, что и скандинавский мастер середины VIII века сначала сделал «золотые» вычисления, и по их результату задал пропорции бронзовому Одину. Очевидно, это произошло бессознательно, то есть интуитивно. А если так, значит, золотое сечение не нуждается в том, чтобы мастер (художник или ремесленник) сознательно поклонялся «золоту». Достаточно, чтобы он поклонялся красоте.
Поющий Один из Старой Ладоги. Бронза. Середина VIII века. Высота Верховный бог Один – не только владелец чудесного копья, но и покровитель песнотворцев. Фигурку Одина на староладожском Земляном городище нашел в 1975 году Е. А. Рябинин. Это – древнейший из известных «портретов» Одина. На торце стержня, которым заканчивается шея Одина, находится прямоугольное отверстие. (По догадке историка Игоря Арзамасцева, перед нами приспособление для подтягивания костяных колков на лире.) Рот Одина полуоткрыт, и кажется, что бог поет. Правый глаз прочерчен двумя концентрическими окружностями. Под лупой они прекрасно видны. Левого глаза нет, но именно левый глаз Один отдал в подземном царстве за возможность испить из источника мудрости. (Благодарю за помощь хранителя ладожского собрания в Государственном Эрмитаже Бориса Короткевича.) А для нас важно, что два ворона (постоянные спутники Одина) не просто сидят у него на плечах, а изображены в виде его рогов, ведь это тоже пример «сворачивания пространства», то есть зрительной полисемии.
А теперь
взглянем на зримо геометризированную «Березовую рощу» Архипа Куинджи,
написанную в Акцентные
точки приходятся не только на два из четырех золотых пересечения (комли двух
центральных берез), но и на √2 (желтая сетка – по нижней горизонтали
граница тени и комли еще четырех деревьев, а по вертикали ствол одной из
берез) и две горизонтали √5 (выделены красным – по горизонтали дальний
край поляны и высота дальних деревьев, по вертикали граница крон левой группы
деревьев). Вряд ли художник специально рассчитывал эти соотношения (ему это просто не нужно, ведь алгоритм его работы – от вдохновения к гармонии, а не от анализа к имитации). Но они гармоничны, и формула этой гармонии не в золотом сечении, а в синтезе золотого сечения, √5 и √2 и других гармонических констант. Во всяком случае у Куинджи синтез переходов цвета и геометрии построен именно на пересечении этих иррациональных величин. Но, может быть, эта закономерность относится только к творениям европейской культуры? Однако обратимся к японской живописи.
Книжная иллюстрация. Япония. XII век. А теперь сравним с древнерусской миниатюрой:
Смерть Вещего Олега. Миниатюра из
Радзивилловской летописи. Копия конца XV века с оригинала XII века.
Александр
Иванов. Явление
Мессии (Явление Христа народу). 1836–1857. Холст, масло. 540 х 750 Государственная Третьяковская галерея Но вот «Явление Христа народу» Александра Иванова. Явственный эффект приближение Мессии к людям возникает из-за того, что он уже прошел точку золотого сечения (перекрестье оранжевых линий) и сейчас входит в ту точку, которую мы будем называть точкой серебряного сечения (это отрезок, деленный на число π, или отрезок минус отрезок, деленный на число π). Именно такие отношения не статичных, а динамических пропорций нередко оказываются у тех произведений, которые и построены на динамике события. Приведу для примера две современных фотографии.
Крокусы. Пасхальная открытка Никиты
Чернова. 2007
На фотографии крокусов под снегом (Подмосковье, весна 2007 года) динамика достигается тем, что два оранжевых венчика устремлены к линии золотого сечения.
«Глазок» (староладожская бусина XI–XII вв.). Снимок и кадрирование Андрея Усова. Желтые линии √2, сиреневые – серебряное сечение, оранжевые – золотое сечение А при анализе трех портретов Работы Леонардо да Винчи оказывается, что у них практически идентичная композиция. И построена она не на золотом сечении, а на √2, горизонтальная линия которого на каждой из трех работ проходит через кончик носа.
√2 в трех портретах кисти
Леонардо да Винчи. Эти примеры можно было бы заменить десятками других. Они показывает, что тенденция свести гармонию к голому «золоту» чревата опасным самообольщением исследователя. Золотые пропорции в совершенном произведении искусства он, скорее всего, отыщет. Но не заметит (потому что не искал) именно того, что и делает данное творение шедевром, и решит, что симметрия (пусть гармоническая) – это и есть сама гармония. Что общего у расположения полипептидных
цепей нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов
млекопитающих, и далеких космических галактик?
Ответ известен: структура, основанная на логарифмической спирали. Т.
Кук открыл роль золотой логарифмической спирали в строении растительных и
животных объектах.[1],
доказав что феномен роста в биологических объектах связан со спиралями
золотого сечения.
Что такое золотая логарифмическая спираль? В ее основе золотой прямоугольник: Последовательно отрезая от него квадраты и вписывая в каждый по четверти окружности, мы и получаем золотую логарифмическую спираль[2].
Золотая логарифмическая спираль. В начале В 1920-х Павел Флоренский рассматривает золотое сечение в качестве
структурного инварианта природных систем (третья глава его книги «У
водоразделов мысли»). Сергей Эйзенштейн, с увлеченностью неофита вычислял
точки золотого сечения в лирике Пушкина, суриковской «Боярыне Морозовой» и
посвятил свою теоретическую работу «Неравнодушная природа» не кому-то, а
«бедному Сальери»[4]. Как писал сам Эйзенштейн, раскрашенный на черно-белой пленке вручную
красный флаг взвивается на мачте восставшего броненосца не где-то, а в
отсчитанной от конца фильма точке золотого сечения (то есть, если весь текст
принять за единицу, формула апогея по Эйзенштейну 1 : Ф2). Альберт Эйнштейн специально золотой
пропорцией не занимался, но заявил, что «эта гамма пропорций... делает зло
трудно, а добро легко выполнимым». Ле Корбюзье в XX
веке проектировал по золотой пропорции дома.
Однако жить в типовых зданиях, разработанных на основе его
«модулора», весьма неуютно. (В СССР этот тип строений прозвали хрущобами.)
Так, может, «Божественная пропорция» не столь уж и божественна? После Второй мировой войны о золотом сечении стали забывать. Но во второй половине XX века специалисты в различных отраслях знаний, в том числе и в биологии, вновь принялись за изучение этой, вроде бы уже решенной проблемы. И настоящий бум исследований начался с 80-х, когда накануне распада СССР золотое сечение стало восприниматься как универсальный принцип самоорганизующихся природных и технических систем. Сошлюсь и на исследования А. П. Стахова, который занимался задачами математической теории измерений. СССР это, впрочем, не спасло. В начале 2006 г. на сайте
новосибирских зодчих[5]
появилась и вызвала горячую дискуссию глава из А. В. Радзюкевича «Законы
красоты – мифология или технология?» Автор пишет: «Считается, что пупок делит
человеческое тело по вертикали на две неравные части в “золотой” пропорции,
т.е. 0,618. Данное допущение, выдвинутое А. Цейзингом полтора столетия назад,
к настоящему времени превратилось в своеобразный краеугольный камень гипотезы
“золотого сечения”. Количество работ содержащих данное допущение так велико,
что не поддается какому-либо учету. <...> В качестве одного из итогов
такого «размножения» стала разработанная в 40-х годах прошлого века
французским архитектором Ле Корбюзье система пропорций человеческого тела
«Модулор» в котором основные размеры увязаны друг с другом в пропорции
”золотого сечения”». Исследователь скрупулезно анализирует несколько десятков примеров канонических для разных эпох изображений человека (от Древнего Египта до рисунков Леонардо да Винчи и Дюрера) и ни в одном из них не находит золотых пропорций[6].. активно обсуждалась членами «Международного Клуба ЗолотогоПодводя итоги дискуссии, президент клуба Алексей Стахов, заключает: «По-видимому,
необходимо разделять ”Законы Гармонии Природы” и “Законы Красоты Искусства”.
“Законы Гармонии Природы” объективны и отражают стремление природных структур
к “оптимизации”, “целесообразности”, экономии вещества и энергии. Как
показывают современные исследования, “Законы Гармонии Природы” тесно связаны
с Золотым Сечением и числами Фибоначчи, причем эта связь обнаруживается на
квантово-механическом и генетическом уровнях. Что касается “Законов красоты”,
то эти “законы” субъективны, так как выражают вкусовые и религиозные
предпочтения определенных групп людей. И вряд ли в этом направлении можно
построить какую-то стройную теорию»[7]. Однако оппозиция «объективная гармония»/«субъективная красота» – типично детское заблуждение (см. эпиграф к этой книге). Недаром, физики любят повторять вслед Альбертом Эйнштейном, что если формула красива, то она верна. А. П. Стахов считает, что «ученый должен верить в Гармонию Мироздания». И в подтверждении этого цитирует Альберта Эйнштейна: «Религиозность ученого состоит в восторженном преклонении перед законами гармонии». Но это совсем не то же самое, что «верить в Гармонию Мироздания». Тезис Эйнштейна при всей своей парадоксальности сугубо научен: религия ученого – познание, а, значит, постижение законов гармонии. Тезис Стахова внятно догматичен и сквозь него проступает до боли знакомое. Мол, должен верить, вот и верь. И обоих случаях возникает вопрос о природе гармонии. А. П. Стахов отвечает на него весьма уклончиво: «Все структуры природы стремятся к “гармоничному”, то есть “оптимальному” (с некоторой точки зрения) состоянию». «С некоторой» – это с какой? Читаем дальше: «С гармонией, как правило, связывают принципы симметрии в живой и неживой Природе». Из контекста ясно, что с этим мнением А. П. Стахов вполне солидарен. И если встать на эту позицию, то цепочка рассуждений должна быть такой: принципы симметрии связаны с гармонией, а золотое сечение – это высший симметрологический и гармонический принцип Бытия. Следовательно, гармония – это золотое сечение. «Мир неживой природы – это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир живой природы – это прежде всего мир гармонии, в которой действует «закон золотого сечения» – можно прочитать на сайте виртуального «Музея золотого сечения». Итак, понятие «Гармонии Природы» сводится к понятию золотого сечения[8]. Однако если гармония – это золотое сечение, а золотое сечение – высший принцип симметрии, то гармония – это... симметрия. К тому же из последней цитаты следует, что красота, каким-то немыслимым образом противопоставленная гармонии, – атрибут симметрии, а не гармонии. Но разве мало в той же виртуальной кунсткамере экспонатов, свидетельствующих о том, что «закон золотого сечения» очень даже «действует» в мире неодушевленных сущностей? Во всей этой путанице,
виноват, видимо, Адольф Цейзинг, который считал, что пропорциональность есть
отношение двух неравных частей между собой и к целому в наиболее совершенном
их сочетании, и так сформулировал свой «Всеобщий закон пропорциональности»: «Деление целого на неравные части пропорционально,
когда отношение частей целого между собой то же, что и отношение их к целому,
т.е. то отношение, которое дает золотое сечение». Почувствуем разницу: то,
что для Евклида лишь «среднепропорциональное деление», для философа времен
промышленной революции и тотальной стандартизации – закон пропорциональности
вообще. Из «закона» Адольфа Цейзинга следует, что пропорциональность может
быть или золотой, или никакой. В середине позапрошлого века идея золотого сечения стала для
математической эстетики Цейзинга тем же, чем для марксиста классовая борьба и
диктатура пролетариата. Не зря же «закрывая дискуссию» с Радзюкевичем, тот же
А. П. Стахов пишет: «Главная идея моих статей и статей других членов
Международного Клуба Золотого Сечения, принявших участие в дискуссии, состоит
в следующем: Золотое Сечение является важнейшим фактором современного
научного и экономического развития». И еще: «Я считаю, что одной из важнейших
тенденций современной науки является глобальная фибоначчизация научного и
экономического развития».
Сказано, увы, безо всякой иронии.
Разумеется, при таком подходе о критическом отношении к предмету
исследования речь не идет: соблазн найти еще один золотой самородок слишком
велик и отдает тем, что психологи называют «сверхценной идеей». Ее
перерождение в чистый миф и дальнейшее вырождение в догму предопределено
начальной установкой – сведением всего многообразия гармонической палитры к
золотому сечению, единственно верному, всепобеждающему и всезеленеющему.
«Вера в золотую гармонию» подчас оказывается столь сильна, что не проверяются
и заведомо сомнительные результаты. Скажем, со ссылкой на книгу химика Н.
Васютинского «Золотая пропорция» (М., 1990) авторы «Музея золотого сечения»
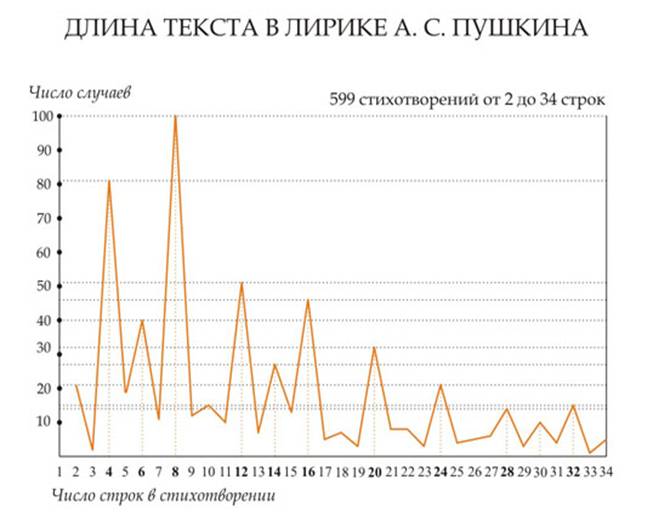
утверждают: «анализ стихотворений А.С. Пушкина с
этой точки зрения показал, что размеры стихов распределены весьма
неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21
и 34 строк (числа Фибоначчи)».
Однако и это – миф.
Возьмем первый том популярного пушкинского трехтомника (М., 1985), в
который вошла практически вся лирика поэта, начиная с лицейской (1813–1836).
В томе 599 законченных и относительно законченных стихотворений (русских и
французских), длина которых не превышает 34 строки. Ограничимся такой длинной
текстов, поскольку выше этого предела практически все случаи единичны.
Увы, не все то золото... Точки 5, 13 и 21 приходятся как раз на
минимумы, и понятно, что никакого анализа не проводилось: просто, заметив,
что у Пушкина чаще всего встречаются восьмистишия (а 8 – число Фибоначчи),
автор решил, что и стихи пишутся по алгоритму размножения кроликов.
А пушкинский ряд совсем другой, ведь основной строительный кирпичик
пушкинской поэзии – четверостишие:
4; (6;) 8; 12; (14;) 16; 20;
24; 28; 32
И практически все пики приходятся на стихи с четным числом строк, а все минимумы на нечетное (что ж, мистики в этом нет, просто парность – это природа рифмы). Однако пропорциональное золото, как правило, обнаруживается именно там, где не ждешь. Вот и при ровно ста восьмистишиях в томе 81 стихотворение в четыре строки: 100 : 81 =
1,235 → √5 – 1 = 1,236 Третий по величине пик приходится на стихотворения в 12 строк. Их 51:
81 : 51 = 1,59 → (√5 + 1)
: 2 = 1,62 Итак, число восьмистиший
больше в 2/Ф раз числа отдельных четверостиший, а тех в свою очередь
в Ф раз больше, чем
двенадцатистрочных стихотворений. Именно в такой пропорции по причинам,
разумеется неведомым и самому поэту, он предпочитал одну стихотворную форму
другой. И числа Фибоначчи тут ни
при чем. Магическое отношение к числам
Фибоначчи – характерная черта «золотого клуба». На
его сайте можно прочитать, что И. Степанов обнаружил ряд Фибоначчи в профилях
почв. Он установил, что на территории
Советского Союза от Карского моря до Каракум мощности гумусового слоя в
пустынном светлоземе в среднем около 5 см, в серо-бурой почве 8, в бурой
полупустынной 13, в светло-каштановой
21, в темно-каштановых почвах 34, в обыкновенном черноземе 55 и
в выщелоченном черноземе 89. А затем от серых лесных и подзолистых
почв к тундровым – падение толщины: 55, 34, 21, 13, 8, 5 см. Но о чем это говорит? Об «объективности» метра? Или о том, что построенная некогда эмпирически классификация почв блестяще выдержала проверку числами Фиббоначи (то есть сама классификация была, пусть и неосознанно, основана на этом математическом ряду)? И то, что у
гавиалового крокодила Малайского архипелага вдоль туловища расположены 55
роговых пластин, на теле кавказской носатой гадюки 55 темных пятен, а в
скелете габонской гадюки насчитали 144 позвонка, – ровно ничего не значит.
Тем более, что поклонникам Фибоначчи то и дело приходится оговариваться:
«Число костей скелета в различных частях тела у самых разнообразных животных
близко (! – А. Ч.) к 13 (кит,
верблюд, олень, тур и т.д.), число позвонков близко (!) к 34 и 55». С такой же
убедительностью можно апеллировать к тому, что на территория СССР встречалось 55 видов змей (а это действительно
так). Современные млекопитающие – это около 3500 видов
(а некоторые зоологи насчитывают и 4250 видов). Каталог океанических обитателей – 200 тысяч видов.
Прибавим 8,6 тысяч видов птиц, 15 тыс. 304 вида рыб и
2500 видов змей и т. д.
А потому даже при среднестатистическом распределении обнаружатся
тысячи случаев совпадений числа костей, хрящей или чешуек с числами любого
математического ряда.
И если в Тихом океане обитают морские звезды астеридеи с 8 лучами, у
так называемой мохнатой звезды 13 лучей, у гелиастера 33 луча, у пламенистой
звезды 55, из этого еще нельзя сделать вывод, что «у многих морских звезд
количество лучей задается числами Фибоначчи или близкими к ним числами».Речь
не о том, что числа Фибоначчи не участвуют в эволюции земной фауны, а о том,
что при данном уровне аргументации разговор не может быть серьезным (то есть
научным).
Даже автор обзорного труда о золотом сечении В. И. Коробко, мужественно
признает, что «...мы пока не в состоянии строго объяснить феномен золотого
сечения»[9].
Однако полагает, что дальнейшее обнаружение золотопропорциональных
закономерностей приближает нас к разгадке.
Перед нами то, что в XX веке американский теоретик науке Томас Кун назвал кризисом парадигмы. Такое бывает, когда ныне существующее
представление о каком-либо предмете или явлении уже не выдерживает напора
«аномальных фактов». А это в свою очередь означает, что без попытки
принципиально нового объяснения данного феномена его дальнейшее изучение практически ничего не даст. Андрей
Радзюкевич пишет: «Даже архитектор И. В.
Жолтовский (советский академик архитектуры, поклонник золотого сечения – А. Ч.) понимал, что «золотая»
Жар-птица не может летать везде. Он утверждал, что если тухлую колбасу
разрезать в золотом сечении, то от этого она не станет свежей». Увы, многие адепты пропорционального золота готовы это оспаривать, ведь по их представлениям в «золотых» пирамидах бритвенные лезвия затачиваются сами собой, а колбаса и вовсе не тухнет. Однако
правда и не на стороне новосибирского зодчего и его единомышленников. Вернемся к одной из старых книг, на которую мы уже
сослались. В
апреле 1935 года главная редакция строительной литературы ОТНТИ
(«Объединенного научно-технического издательства») выпустила том, на титуле
которого можно значится: «Проф. Г. Д. Гримм. Пропорциональность в
архитектуре. Ленинград–Москва». И хотя ссылку на эту книгу найдешь почти что
в каждой полемике о золотом сечении, чем дольше листаешь эту монографию, тем
сильней уверенность, что штудировали ее, что называется «с карандашом»,
совсем не многие. В
предисловии об авторе сказано лишь то, что профессор Гримм более сорока лет занимается
теорией пропорции, и перед читателем итог его научных разысканий. На
исходе XIX столетья начав в рядах сторонников «классической
схемы пропорциональности», Грим в конце концов увлекся золотым сечением и на материале
десятков памятников древности, средневековья, барокко и современности (вплоть
до анализа проектов Дворца Советов в Москве) показал, что основанная на
пропорциях октавы классическая схема золотому закону Цейзинга (римский канон
Витрувия дает результат, весьма близкий резульат). Происходит это и потому,
что приближение к золотому сечению содержится в самих интервалах октавы, и
потому что «золотое сечение» – объективный закон гармонического природного
членения. Профессор не знает, когда именно архитекторы перешли от принципа
гармоничного музыкального членения к золотому, но показывает, что с древности
«интуитивное ощущение» золотого закона определяло пропорции построек. Еще не
подозревая о том, сколь ярые формы в самые ближайшие годы примет «борьба с формализмом»,
редакция лишь мягко журит автора за то, что «проблема пропорциональности и
принцип “золотого сечения” в архитектуре трактуется в книге несколько
отвлеченно», а «момент пропорциональности освещается оторвано от общей
композиции и стиля архитектурного сооружения». Однако
это не правда. Профессор с того и начинает: «Основой каждого вновь созидаемого сооружения, каждого
архитектурного памятника является: с одной стороны – его наибольшая
целесообразность, ясность и простота при оправдании архитектурных его форм,
принятых в соответствии с материалом и его назначением, с конструкциями и
прежде всего его внутренним содержанием; с другой – определяющий ценность
здания в художественном отношении, правильный учет
художественно-композиционного момента и (в этом месте на полях книги
явственен запах редакторского клея – А.
Ч.) четкое решение проблем идеологического восприятия форм современности»
(с. 7). (Впрочем, во всей монографии
Гримма, это единственный поклон в сторону современной ему политической реальности
и сильных сего мира.) Начав
с исторического очерка развития теории пропорциональности, Гримм вводит в
деление целого отрезка по золотому сечению два термина – мажор («майор») и
минор. Исследователь показывает бесконечность золоточисленной лестницы (геометрической
золотой прогрессии): при делении на 1,618… на следующей ступеньке каждый
минор становится мажором: 1; 0,618…; 0,382…; 0,236…; 0,146…; 0,090…; 0,056…;
0, 0034… и т. д. Но
можно пойти и вверх по этой лестнице: 1; 1,618…; 2,618…; 4,236…; 6,854…; 11,090… При
делении горизонтального (или вертикального) отрезка по золоту на первом шаге
есть лишь два решения: минор может быть слева (внизу) или справа (вверху). Но
уже вторичное деление позволяет получить несколько комбинаций. Как же
добиться гармонии целого и частей? «Выполнение этих требований достигается архитектурной
композицией, которая заключается в создании проекта сооружения, составленного
путем сочетания их в одно архитектурное целое. При этом одним из основных
моментов художественного оформления сооружения является достижение гармонии
здания, которая слагается из ряда отдельных факторов – симметрии и
асимметрии, ритме и контрасте, масштабности, соразмерности и равновесия,
регулирующим звеном которого является пропорциональность. <…> В беспредельной
области творчества опорные точки необходимы: как музыка подчиняется законам
колебания звука, так и архитектура должна подчиняться своим законам, и только
соблюдение их в архитектурном произведении дает художественное целое» (с. 7). Развивается
эта простая в сущности мысль и дальше. Солидаризируясь с французским
теоретиком середины XIX века
Виоллетом Ле-Дюком, Гримм цитирует: «Большое
достоинство греческих зодчих состояло в том, что у них были выработаны законы
пропорциональности в архитектуре и что греки им подчинялись, несчастье нашего
времени составляет убеждение, что архитектурное произведение может быть
создано, руководствуясь одним лишь воображением, одной лишь фантазией,
подчиняясь единственно так называемому вкусу, одним словом так, как создается
туалет красивой женщины» (с. 9). Гримм
пишет о трех египетских канонах. Первый, по его мнению, древнейший,
относящийся к времени правителей IV или V династии, найден археологами в Мемфисе. В нем
человеческая фигура до лба разделена на шесть частей, равных длине ступни
(одному футу). Второй канон относится к XVIII династии. (Здесь каждая из шести частей разделена
еще на три.) Третий канон, времени Птолемея, обнаружен комиссией
наполеоновских ученых: на нем фигура человека до лба составляет уже семь футов,
а каждый фут поделен еще на три части. Но число 21, как замечает Гримм, дает
возможность наиболее близко подойти к золотой пропорции (13/8). (Заметим
однако, что речь идет, строго говоря, не о пропорциональном, а строительном
каноне, то есть о числе каменных блоках, составляющих тело статуи.) Гримм
ссылается на Плутарха: «Особое
значение египтяне придавали прямоугольному треугольнику со сторонами 3 и 4 и
гипотенузой 5, с помощью которого могут быть построены интервалы всех целых
тонов октавы. Плутарх в трактате об Исиде и Осирисе (глава 56) отмечает, что
египтяне представляли вселенную в виде такого прямоугольного треугольника,
приравнивая вертикальный катет 3 мужскому роду, основание 4 женскому, а
гипотенузу – ими сотворенному: вертикаль – Осирису, основание – Исиде,
гипотенузу – Гору» (с. 10). При
помощи этого треугольника египтяне и получали основные пропорции. Еще
цитата: «Витрувий в своем трактате об архитектуре перечисляет
употребительные у математиков древности сравнения музыкальных интервалов с
отношением углов правильных фигур, дающих подобные же отношения; так, он
сравнивает октаву с отношением угла правильного треугольника к углу
правильного шестиугольника: 60: 120, как 1 : 2; квинту – с отношением угла
правильного треугольника к углу правильного четырехугольника: 60 : 90 или 2 :
3; кварту – с отношением угла правильного четырехугольника к углу правильного
шестиугольника 90 : 120, или 3 : 4. <…> По стопам египтян пошел
Пифагор. Ему приписывают установление двух основных законов гармонии в музыке,
принятых греками: 1) два звука дают гармоническое созвучие, если отношение их
колебаний выражается малыми числами; 2) гармоническое трезвучие получается,
если к аккорду из двух консонансных звуков придать звук, число колебаний
которого находится в гармонической пропорциональной связи с двумя первыми.
Грекам во всяком случае были известны связь между музыкальным звуком струны и
длиной этой последней; они более или менее точно выяснили численные
соотношения главных музыкальных созвучий и на этих основах установили свою
теорию гармонии, строили свои музыкальные инструменты, поверяли также и
пропорциональность своих архитектурных памятников. <…> Заметим, что
деление целого отрезка по золотому сечению находится между квинтой и секстой.
<…>» (с. 69). Тем
неожиданней вывод профессора Гримма: «Однако отношения непосредственно пропорционально между собой
связанных архитектурных частей целого в классических памятниках согласованы
почти исключительно по интервалам, наиболее приближающимся к золотому
сечению, по интервалам от кварты до октавы». <…> В разобранных нами
архитектурных памятниках Греции и Рима в последовательно между собой
связанных архитектурных частях удалось установить: чаще всего – до 100
случаев – применение отношения 2 : 1, т. е. октавы, а также квинты 3 : 2;
более 50 случаев применения отношения 4 : Гримм
показывает, что к золотой пропорции ближе всего уменьшенная секста (8 : 5); и
еще несколько интервалов с более или менее незначительными погрешностями
соответствуют делению интервала октавы на Ф2,
Ф3… Ф7. Это увеличенная терция (125 : 96 = 1,302 = Ф2/2); увеличенная секунда
(75 : 64); терция (5 : 4); уменьшенная терция (6 : 5); увеличенная прима (25
: 24). Но
«приближающиеся к…» на значит «те самые». Тем более что при известной
ловкости, деля, складывая и вычитая,
можно получить практически любое число. Гримм задается вопросом, почему
греки, зная о золотом делении, совсем не часто его использовали? И сам себе
отвечает: «Причина, почему зодчие классики тем не менее не приняли его, а
довольствовались более или менее близкими к нему численными приближениями,
лежит без сомнения как в том, освященном веками значении, которое придавалось
численным отношениям интервалов октавы, признававшимся постоянными
величинами, обусловливающую всякую гармонию, так и в простоте их применения.
К тому же золотое сечение, геометрически простое и четкое, дает все же
неприемлемые для древних греков иррациональные численные величины» (с. 70). Видимо,
эта промежуточность в позиции профессора (то, что называется сидеть на двух
стульях) и способствовала тому, что книга Гримма осталась как бы в
стороне от магистрального пути изучения пропорций. Но и
сегодня теоретического обоснования гармонии не существует. А, значит,
профессиональные секреты профессии архитектора столь же зыбки и столь же
беззащитны, как и в седом средневековье.
Гримм пишет: «Эпоха готического зодчества без всякого сомнения пользовалась
определенной, выработанной ею системой пропорциональности, которая при этом
являлась франкмасонской тайной. Насколько ревностно эта тайна оберегалась,
видно хотя бы из старого предания, по которому в Гримм
анализирует башню собора в Ульме (начало строительства Этот
же феномен исследователь обнаруживает и в памятниках древнерусского зодчества
московского времени, и в Смольном соборе Растрелли. Однако приведенные
Гриммом чертежи свидетельствуют, что оговорка об «интуитивности» – вряд ли
что-то более, чем реверанс в сторону рецензентов, редакторов и цензоров.
(Чего стоит одно лишь малограмотное примечание от редакции на с. 78,
гласящее: «Хотя сущность примитивной геометрии, существовавшей в Египте,
наукой не установлена до настоящего времени, все же “теоретическое знание
таких математических проблем, как золотое сечение” предполагает более
развитое состояние геометрии и математики, чем то, о котором история
предполагает для Египта данного периода».) Сетуя
на «невыясненность общих законов пропорционирования», Гримм не забывает
подчеркнуть, что золотой принцип существует лишь как некая природная данность,
а задача архитектора использовать ее в своих целях и для выражения
собственной архитектурной мысли. Профессор утверждает, что проектировать «по
золоту» нельзя. Надо лишь корректировать золотыми отношениями пропорции
целого и частей, то есть, разрабатывая первоначальный эскиз, перепроверить
его по золотой шкале: «Проверка принятых интуитивно и на основе композиционных
требований, на первом этапе проектировки, отношений отдельных масс, отдельных
архитектурных частей между собой, должна внести ту закономерность, тот высший
порядок, ту гармонию целого, которая и составляет особую ценность
архитектурно-художественного памятника» (с. 134). А вот
и вывод: «Выясненное выше в нашем изложении исключительное значение в
смысле пропорциональности деления золотого сечения как первичного, так и
высших порядков, производного деления по схеме геометрической прогрессии
золотого сечения, простая практическая применимость ее, гибкость в подходе к
композиционным началам, принятым предварительно эскизным проектом, наконец,
установленное интуитивное ее применение в отношении архитектурных частей
выдающихся памятников прошлого, выдвигает схему золотого сечения на первое
место. <…> Основанная на законе золотого сечения пропорциональная схема
геометрической его прогрессии дает широкую возможность получения самых
разнообразных делений, самых разнообразных членений архитектурного целого на
пропорциональные между собой части. Полное пропорциональное равновесие
архитектурного целого достигается соблюдением неразрывной пропорциональной связи
общего со всеми его деталями…» (с. 135). Можно
было бы записать Гримма в число адептов и продолжателей Цейзинга. Но это не
вполне соответствует действительности. Гримм пишет: «Особое внимание Цейзинг уделяет развитию его теории в
отношении пропорций человеческого тела, попутно освещая значение золотого
сечения в других проявлениях последнего – в музыке, в растительном мире, в
мире животных, в строении минералов, а также в архитектуре. Однако его
несколько примитивный подход к пропорциональному разбору архитектурных
памятников дает неубедительные результаты и является причиной непризнания его
схемы» (с. 8). Эту
вот примитивность непрофессионала Гримм и сумел преодолеть. От идеи «музыки в
камне» он ушел к идее природной пропорциональности архитектуры. И тем
оставил место для возможности усовершенствования и развития своей теории.
Десятки приложенных к монографии Гримма чертежей и проанализированных им
строений доказывают, что, сочиняя свою антисказку («Красивая сказка о золотом
сечении»), новосибирский теоретик Андрей Радзюкевич, хоть и подметил многие
частные ошибки адептов золотого сечения, с выводами все же поторопился. После
книги профессора Гримма стало ясно, что архитектурный канон, который
тысячелетиями вырабатывало человечество, оказался частным случаем
математического канона природной пропорциональности.
Смольный
собор в Петербурге. Пропорциональный
анализ золотого сечения по Г. Д. Гримму. Уже в
наше время корректность основных выводов Г. Д. Гримма была подтверждена многими
исследователями. Остановимся только на одной публикации в немецком журнале (Burgen und
Schljsser. 1987. № 1.), который
открывается публикацией Михаила Мильчика и Ольги Гусевой о золотых пропорциях
крепости и церквей в Иван-городе, построенной итальянскими мастерами при
Иване III (строительство начато в 1492 году от Рождества
Христова, то есть в роковом и последнем, как представлялось современникам,
7000 году от Сотворения мира). Питерский
архитектор-реставратор О. Г. Гусева познакомила меня и с текстом более
подробного своего исследования, которое еще только готовится к печати
(«Соразмерность архитектурных форм Ивангородских церквей, построенных
итальянским зодчим».)
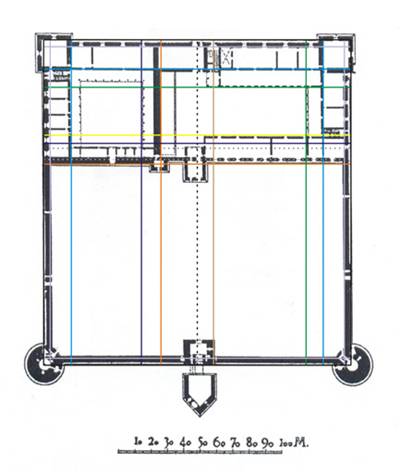
Ивангородская
крепость по О. Г. Гусевой О. Г. Гусева
приводит три ряда пропорций, увеличивающихся по коэффициенту 1,618. Для
примера приведем один из рядов (по обмерам): 1,93
(по другому обмеру 1,98) м – 3,2 (3,14) м – Если
учесть, что При
такой стройности практического результата и теоретической данности говорить
об «интуитивном» использовании золотой пропорции было бы наивно. P.S. В конце августа 2007 года на Земляном городище Старой Ладоги
по моей просьбе археологи сделали обмеры нижних венцов деревянного «большого
дома» (середина X
века). Дом оказался золотым: 13,43 на 8,3 м. Золотое число 1,618... – не где-то, на севере языческой еще
Руси… В Питере над этим сюжетом больше всех смеялась
архитектор-реставратор Ольга Гавриловна Гусева: именно такие размеры у
Никольской церкви в Иван-городе (напомним, это конец XV века, итальянские
мастера). Приведу
еще два «золотых» примера из наследия итальянского зодчества XIV–XV веков.
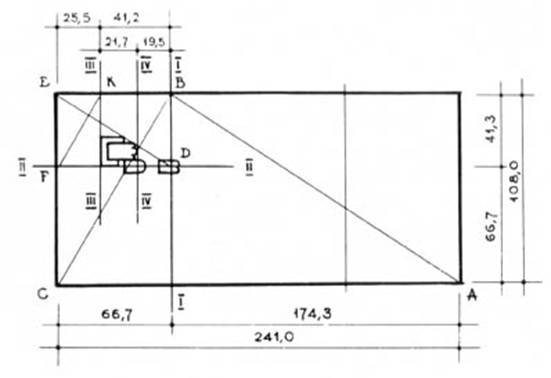
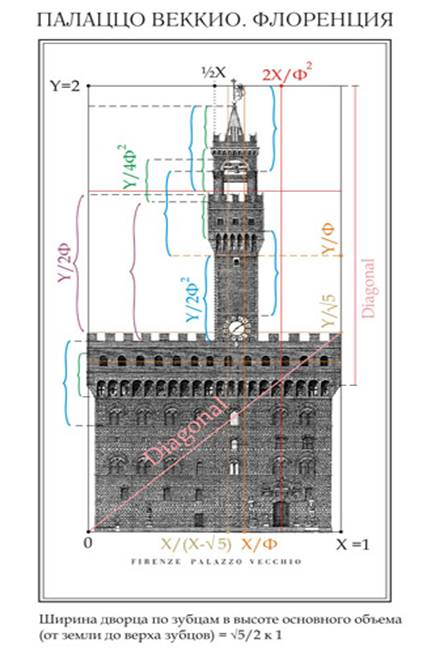
Здание
городского самоуправления во Флоренции Палаццо Веккиа. Построено
между 1299 и 1314 гг.
Замок
Сфорца (Castello Sforzesco или Castello Sforza). Милан. XIV–XV вв. |