Правка 29 апреля 2009

Андрей Чернов. ЗАМЕТКИ О ВЕЧНОМ

– Ну почему опять в Кунсткамеру, а не в Эрмитаж?

– Видишь ли, папа, я творчество природы люблю больше творчества человека.

Из разговора с восьмилетней дочерью

Тебе числа и меры нет.

Державин

ПРИНЦИП ДИАЛЕКТИЧЕСКОГО ИМПЕРАТИВА

(О золотом сечении, эволюционном механизме ряда Фибоначчи и одной ошибке Гегеля)

В 1202 году тридцатилетний итальянский купец и путешественник Леонардо из Пизы по прозвищу Фибоначчи[1] написал «Книгу абака» (Liber abacci), в которой познакомил европейцев с арабскими цифрами (арабы, впрочем, заимствовали их у индийцев) и с понятием нуля.

В книге содержалась и такая задачка о размножении кроликов:

«Сколько пар кроликов рождается в один год от одной пары? Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рожают кролики со второго месяца после своего рождения. <...> Мы складываем первое число <родившихся пар> со вторым числом, т.е. 1 и 2; и второе с третьим; и третье с четвертым; и четвертое с пятым; и так одно за другим, пока не сложим число десятого <месяца> с одиннадцатым, т. е. 144 с 233,[2] и мы получим общее число упомянутых кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев».

В ряду Фибоначчи каждое следующее число, начиная с третьего, является суммой двух предыдущих.

F _n = F _{n – 1} + F _{n – 2}

Начало ряда Фибоначчи обычно начинают с единицы (реже – с нуля):

(0); 1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377…

По Фибоначчи математику учили до XVII столетия. Было замечено, что отношение смежных чисел ряда Фибоначчи стремится к той пропорции, которую сегодня называют золотым сечением. Полагают, что это наблюдение принадлежит Иоганну Кеплеру (1571–1630). Позднее это строго доказал Р. Симпсон (1687–1768).

И впрямь, 8 : 5 = 1,6, а 377 : 233 дает уже приближение к числу золотого сечения до пяти знаков по запятой 1,61803...

В 1728 году работавший в Петербургской Академии Наук швейцарец Даниэль Бернулли (1700–1782) опубликовал формулу, определяющую n-член ряда Фибоначчи. Однако она была позабыта, и в 1843 г. заново выведена французским ученым Жаком Филиппом Мари Бине (1786-1856):

Ф ⁿ – (–1) ⁿ  Ф ^—n 

F _n = ––––––––––––––

√5

где n = 0; ±1; ±2; ±3…

В XVII столетии Фибоначчи входит в моду. Во всяком случае, в среде тех, кто изучал тайны неба. Современник Кеплера астроном Джованни Доменико Кассини (1625–1712) доказал тождество, связывающее три соседних числа Фибоначчи:

F_{n + 1} × F _{n – 1} – F_n² = (– 1)ⁿ        

при n > 0

Это значит, что если взять три смежных числа ряда Фибоначчи, то перемножение крайних минус квадрат среднего будет давать через раз – 1 и + 1.

(Впрочем, ниже мы покажем, что некий «обобщенный ряд Фибоначчи» и начинается вопреки формуле Кассини не с + 1, а с «нулевой пары» – 1; + 1.)

Кеплер – последний романтик и последний алхимик европейского гуманизма. После его смерти о золотом сечении забыли на два века. Средневековая задачка о кроликах, плодящихся каждый раз исключительно близнецами, видимо, показалась несерьезной веку Просвещения, энциклопедизма, промышленных и социальных революций.

Известно, что ряд Фибоначчи обладает фундаментальным свойством среднепропорционального отношения – единством аддитивности[3], мультипликативности[4] и рекуррентности[5]. То есть это одновременно и арифметический ряд и геометрическая прогрессия. Однако все это (в том числе и последовательное приближение пропорции смежных членов к золоту) справедливо для любого ряда, в котором каждый следующий член есть сумма двух предыдущих. Первым, насколько мне известно, это понял исследователь золотой пропорции архитектор-реставратор из Костромы И. Ш. Шевелев[6]. Можно взять два любых числа (скажем, 1 и 100), и через полтора десятка сложений получить пару смежных чисел, отношение которых будет приближено к золотому числу Ф с точностью до шести знаков по запятой.

Рекуррентность и мультипликативность – свойства золотого числа Ф при возведении его в степень N. Напомню, что прогрессия вида 1, Ф, Ф²... Фⁿ – геометрическая (и одновременно арифметический ряд).

Однако, насколько мне известно, ни физики, ни философы до сих пор не обратили внимания на тот простой факт, что единство аддитивности, мультипликативности и рекуррентности эволюционных рядов Фибоначчи и Люка – прямые следствия диалектической триады, которую, преодолевая кантовские антиномии, Фихте сформулировал как тезис и антитезис и синтез (субъект, его отчуждение и его возвращение к самому себе), а Фридрих-Вильгельм Шеллинг осознал как объективный элемент построения мира (что тут же взял на вооружение Гегель, а несколько позже Маркс). Итак:

Теза → антитеза → синтез

Процитирую классика современной философии:

«Диалектика (в современном, то есть главным образом гегелевском, смысле термина) – это теория, согласно которой нечто – в частности, человеческое мышление,– в своем развитии проходит так называемую диалектическую триаду: тезис, антитезис и синтез. Сначала – некая идея, теория или движение,– “тезис”. Тезис, скорее всего, вызовет противоположение, оппозицию, поскольку, как и большинство вещей в этом мире, он, вероятно, будет небесспорен, то есть не лишен слабых мест. Противоположная ему идея (или движение) называется “антитезисом”, так как она направлена против первого — тезиса. Борьба между тезисом и антитезисом продолжается до тех пор, пока не находится такое решение, которое в каких-то отношениях выходит за рамки и тезиса, и антитезиса, признавая, однако, их относительную ценность и пытаясь сохранить их достоинства и избежать недостатков. Это решение, которое является третьим диалектическим шагом, называется синтезом. Однажды достигнутый, синтез, в свою очередь, может стать первой ступенью новой диалектической триады и действительно становится ею, если оказывается односторонним или неудовлетворительным по какой-то другой причине. Ведь в последнем случае снова возникнет оппозиция, а значит, синтез можно будет рассматривать как новый тезис, который породил новый антитезис. Таким образом, диалектическая триада возобновится на более высоком уровне; она может подняться и на третий уровень, когда достигнут второй синтез»[7].

Считается, что диалектическая триада – универсальный принцип любого развития. Но, – обратим внимание! – гегельянцы и постгегельянцы учат, что каждый новый синтез становится для следующей триады новой тезой[8]. Полагаю, что это и есть главная и, может статься, роковая ошибка гегелевской (а после и марксистской) «диалектики».

Аддитивные ряды опровергают заблуждение о диалектическом синтезе, становящемся новой тезой, столь же решительно, как сама диалектика опровергает и схоластику, и метафизику. Традиционное начало ряда Фибоначчи 1 + 1 = 2, но, чтобы дойти до 3, необходимо вернуться на шаг назад: 1 + 2 = 3. То есть, сделав два шага от тезы к синтезу, мы, чтобы продолжить движение вперед, вынуждены на шаг отступить. При этом прежняя антитеза оборачивается новой тезой, а прежний синтез превращается в новую антитезу[9]. Только тогда триадная цепочка не распадается на отдельные звенья, и развитие не прерывается. И только так с каждой следующей триадой мы получаем величины, пропорции которых все более приближаются к золотому идеалу.

То, что золотые пропорции обнаружены в сотнях природных объектов и явлений (от строения кристаллов и расположения семечек в подсолнухе до строения человеческого тела, Солнечной системы и творений ума и рук самого человека), говорит об эволюционной универсальности аддитивных рядов. Триада Фихте-Шеллинга – философский аналог аддитивности, а диалектические метаморфозы эволюционного процесса проистекают по математической схеме аддитивных рядов, и, прежде всего, – по алгоритму начинающегося с двух единиц ряда Фибоначчи.

Проиллюстрируем вышесказанное на модели обыкновенной цепочки.

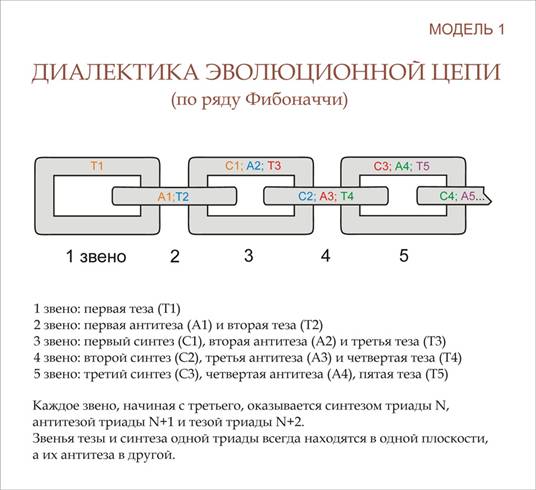
Начиная с третьего, каждое звено триады и само по себе триадно: оно заключает в себе синтез порядка N, антитезу порядка N+1 и тезу порядка N+2.

Меж тем, второе от начала звено в цепи обладает двумя свойствами: это антитеза первой тезе, находящаяся в другом пространственном развороте по отношению и к первой тезе, и к первому синтезу. Но одновременно это звено – теза второй триады.

И только первой звено не содержит в себе свойств антитезы и синтеза.

Начальная теза – чистая теза.

Модель диалектической триады можно представить и в виде одного единственного звена цепочки, взятого по некоторому, пересекающему его вектору временного движения.

Пусть теза – одна сторона колечка, синтез – другая (при замере по прямой обе точки приходятся на металлический пруток, из которого изготовлено звено). А посредине окажется антитеза – дырка. Но и тут, чтобы присоединить еще одно звено, надо продеть новое в предыдущее. И тогда новая теза займет место прежней антитезы, а прежний синтез окажется совмещен с новой антитезой. Другими словами, чтобы кольца сцепились, надо сделать шаг назад, заняв новой тезой пустое пространство прежней антитезы.

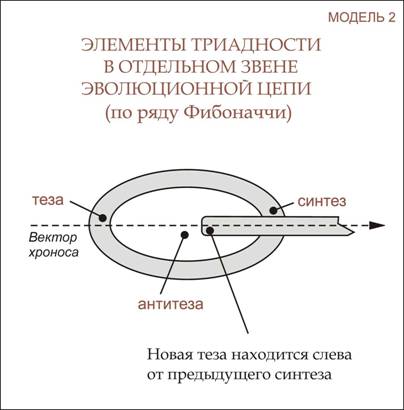
Эта модель вовсе не столь избыточна, как может показаться на первый взгляд, ведь антитезой в ней – сама категория времени. Наше сиюминутное восприятие времени линейно (мы живем в настоящем, помня о прошлом и пытаясь предугадать будущее), а наше переживание времени точечно. На модели видно, почему при таком мироощущении нам будет недоступно не только многомерие, но и даже простейшее двумерие. Двигаясь по временному вектору от тезы и привыкнув к крепкой ее незыблемости, мы вдруг теряем под ногами привычную почву и, прежде чем добраться до синтеза, должны пройти «пустое» пространство антитезы.

Можно предположить, что в многомерном мире переход тезы в синтез обусловлен не антитезой, а тем продолжением внутреннего развития тезы, которое происходит в ином, неочевидном для нас времени и пространстве (на рисунке оно изображено сверху и снизу от временного вектора в виде самого колечка).

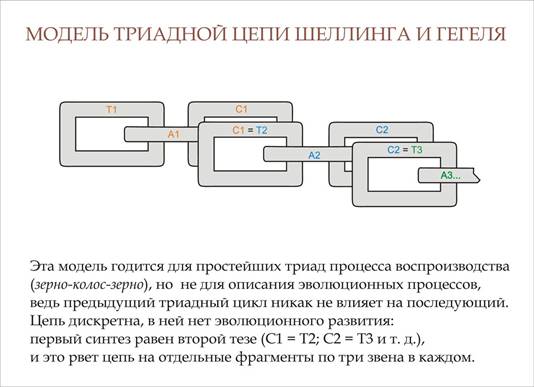
Итак, у нас имеются две возможных модели для описания одного и того же эволюционного процесса. Увы, уже Шеллинг считал, что первый синтез выступает непосредственно в качестве второго тезиса (Фихте, впрочем, в этом уверен не был).

Тем же путем пошли и гегельянцы, и материалисты-постгегельянцы: кольца триадной цепи сдвигаются вплотную или накладываются друг на друга, и эта конструкция объявляется неким цельным единством. (Так дети, рисуя Лукоморье, ученого кота и «златую цепь на дубе том», изображают цепь в виде придвинутых вплотную кружочков.) При столь «детском» подходе, разумеется, становится невозможным и само изучение свойств диалектической триады, которое заменяется выдаваемыми за законы диалектики гегелевскими следствиями о единстве и борьбе противоположностей, отрицании отрицания и переходе количества в качество. Где-то здесь, видимо, и корни «диалектической логики» Гегеля, за разработку которой в одной из статей брался Ленин, а за ним и советские «диалектики», той логики, при посредстве которой марксистское учение перестало быть проверяемым и превратилось в мифологическую догму, в род социально-шизофренического двоемыслия, которое спародировал Оруэлл в сентенциях типа: «война – это мир», «свобода – это рабство», «незнание – сила».

Марксисты к диалектической триаде относились (и относятся) с плохо скрываемым подозрением. Плеханов, к примеру, называл ее «сумасшедшим пустяком». Приведу пространную выписку из одной его работы:

«Теперь мы узнали уже главнейшие отличительные признаки диалектического мышления, но читатель чувствует себя неудов­летворенным. А где же знаменитая триада, спрашивает он, та триада, в которой заключается, как известно, вся суть гегелев­ской диалектики? Извините, читатель, мы не говорили о триаде по той простой причине, что она вовсе не играет у Гегеля той роли, которую ей приписывают люди, не имеющие никакого по­нятия о философии этого мыслителя, изучавшие ее, например, по «учебнику уголовного права» г. Спасовича. Полные святой простоты, эти легкомысленные люди убеждены, что вся аргумен­тация немецкого идеалиста сводилась к ссылкам на триаду; что с каким бы теоретическим затруднением ни сталкивался старик, он с спокойной улыбкой предоставлял другим ломать над ним свои бедные, «непосвященные» головы, а сам немед­ленно строил силлогизм: все явления совершаются по триаде; я имею дело с явлением; следовательно, обращусь к триаде. Это просто сумасшедшие пустяки, как выражается один из пер­сонажей Каренина, или неестественное празднословие, если вам больше нравится щедринское выражение. Ни в одном из 18 томов сочинений Гегеля «триада» ни разу не играет роли довода, и кто хоть немного знаком с его философским учением, тот понимает, что она никоим образом не могла играть ее. У Гегеля триада имеет такое же значение, какое она имела еще у Фихте, филосо­фия которого существенно отличается от гегелевской. Понятно, что только круглое невежество может считать главным отли­чительным признаком одной философской системы признак, свойственный по меньшей мере двум совершенно различным системам.

Нам очень жаль, что «триада» отвлекает нас от нашего из­ложения, но, заговорив о ней, надо кончить. Посмотрим же, что это за птица.

Всякое явление, развиваясь до конца, превращается в свою противоположность; но так как новое, противоположное пер­вому, явление также, в свою очередь, превращается в свою про­тивоположность, то третья фаза развития имеет формальное сходство с первой. Оставим пока вопрос о том, насколько соот­ветствует действительности такой ход развития; допустим, что ошибались люди, думавшие, что — совершенно соответствует; во всяком случае ясно, что «триада» вытекает только из одного из положений Гегеля, но сама вовсе не служит ему основным положением. Это очень существенная разница, потому что, если бы триада фигурировала в качестве основного положения, то под ее «сенью» действительно могли бы искать защиты люди, отводящие ей такую важную роль, но так как она в этом качестве не фигурирует, то за нее могут прятаться разве лишь такие, кото­рые слышали звон, да не знают, откуда он...»[10].

Меж тем, из самого принципа диалектической триады следует, что диалектика может быть только идеалистической, и, следовательно, «диалектического материализма» в природе науки не бывает.

Действительно, для диалектического (объективного) идеализма легко составить самую общую («системную», как сказал бы Рэм Баранцев) триаду, связывающую и Творца, и весь цикл творения (включая сотворение им человека):

Дух → материя → одухотворенная материя (человек)

Но для материалистической парадигмы ничего подобного создать невозможно, не нарушив самой парадигмы. Поскольку в материалистическом коде Дух не является научной категорией, а сознание есть неотчуждаемое свойство наиболее высокоорганизованной живой материи (а, значит, по определению не может выступать в роли антитезы) вариант «Материя → сознание → разумная материя» оказывается лишь инверсированным случаем диалектической триады идеализма.

Из этого и следуют три вывода, которые по аналогии с известной кантовской формулой можно, наверное, назвать диалектическим императивом. Два из них приведем:

a) диалектика (включаем в это понятие и диалектику как метод познания, и диалектический эволюционный механизм метаморфоз всей видимой вселенной) может существовать лишь в идеалистической парадигме;

b) материализм может быть только вульгарным (и более никаким).

Третий – очевиден.

Поскольку связь аддитивности (а, значит, и золотого сечения) с диалектической триадой не была установлена, в золотом сечении нередко видят лишь заурядный геометрический фокус[11]. На самом деле, золотое сечение – что-то вроде реликтового излучения самой эволюции. О чем, собственно, и говорит его восходящая к рекуррентным рядам родословная.

Когда «золото» обнаруживается в творении рук, души и ума человека, можно утверждать, что это творение – следствие эволюционного развития формы.

В начале XX века Резерфорд был поражен тем, что его модель атома водорода оказалась двойником структуры Солнечной системы. Вот и сквозь средневековую задачку о размножении кроликов просвечивает математическая модель механизма эволюции.

Вернемся в крольчатник Фибоначчи. В ряду знаменитого пизанца первая единица означает первопару кроликов (1 = √1√1), а вторая – родившуюся от нее (также √1√1). Каждый кролик сам по себе не единица, а только √1. (Так и числа ряда Фибоначчи необъяснимы вне квадратных корней.) Во всяком случае, с точки зрения природы любая детородящая пара – не две единицы, а два √1, при перемножении дающая единицу. Но неужели же мы должны поверить, что все сущее распространяется во вселенной по формуле размножения кроликов?

Или, может быть, дело совсем не в кроликах?

Кассини, рассматривал классическую последовательность ряда Фибоначчи (то есть ту, что годится для подсчета кроликов), которая начинается с единицы (первопары кроликов), поэтому у него n > 0.

Но Фибоначчи начал свой ряд вовсе не с первого его члена. Покажем, что арифметически этот ряд может быть продолжен и влево. Первую и вторую единицу классического ряда Фибоначчи можно получить, сложив: –1 и 1 (то есть разложив некий Первоноль на –1 и 1).

Запишем:

–1; 1; 0; 1; 1; 2; 3; 5; 8…

А если пойти от первой плюс единицы по числовой оси влево, то получим минус ряд Фибоначчи. В обычной записи слева направо это будет выглядеть так:

1; –1; 0; –1; –1; –2; –3; –5; –8…

Точка отсчета (Первичный ноль) присутствует в виде начальной триады:

[0; (– 1+ 1); 0]

Поскольку (– 1 + 1 = 0), то можно назвать ее Нулевой триадой.

Обобщим, запустив два ряда в обе стороны от исходной точки:

от – 1 Нулевой триады вправо к + ∞

следует «плюс ряд Фибоначчи»

– ∞… ← – 8; – 5; – 3; – 2; – 1; – 1; [0; (– 1 +1); 0;] 1;    1;    2;    3;    5;    8; →… + ∞

от + 1 Нулевой триады влево к – ∞

следует «минус ряд Фибоначчи»

Наша последовательность кроликам уже не подойдет: на ее сегмент, выделенный полужирным шрифтом, закон Кассини не распространяется. Формулой Кассини нулевая триада не описывается.

Материальная магия усердно размножающихся кроликов не оставляла возможности представить, что в нашей Вселенной ряд эволюции может начинаться с отрицательной величины.

Позволим себе пофантазировать: если при творении мироздания процесс начался с появления «антиматерии» (–1) и «материи» (1), то в результате аннигиляции это должно было привести к «Большому взрыву» (обратим внимание на две нулевых точки в нашем ряду справа и слева от первичных единицы и минус единицы). Можно допустить, что так и включись механизмы сразу двух параллельных эволюций: Вселенной и «минус-Вселенной»[12].

Напомним, что и в классическом варианте Кассини три смежных числа ряда Фибоначчи при перемножении крайних за минусом квадрата среднего будет через раз давать то – 1, то + 1, то есть в сумме все тот же мистический ноль (– 1; 1).

В нашем варианте ряда Фибоначчи этот математически не объяснимый тройной «ноль» оказывается именно там, где берут свое начало, разбегаясь в обе стороны от него, две бесконечности – одна «плюсовая», другая «минусовая».

В 1958 г. московский инженер Николай Брусенцов на основании троичной системы счисления сконструировал ЭВМ «Сетунь», а в 1970 году создал новую машину «Сетунь-70».

Современная компьютерная техника основана на двоичном коде 0; 1 (сигнала нет; сигнал есть). Но троичная система, за которой, как полагают эксперты, – будущее, и построена на использовании трех символов, и это – 1; 1; 0 (отрицательный сигнал; положительный сигнал; сигнала нет). А это первые три члена уточненного ряда Фибоначчи.

Существует теорема Джона фон Неймана о том, что среди всех основных позиционных  систем счисления именно троичная позволяет наиболее эффективно сворачивать информацию. В последние годы основные параметры компьютерной техники ежегодно вырастали в среднем в 1000 раз за 5 лет. Бесконечно это продолжаться не будет (помешает атомарное строение вещества) и, как полагают эксперты,  лет через десять или пятнадцать производители компьютерной техники вынуждены будут отказаться от двоичной системы счисления в пользу троичной.

В одном из последних своих интервью Николай Петрович Брусенцов (сегодня он заведующий лабораторией ЭВМ факультета Вычислительной математики и кибернетики МГУ) утверждает: «Если мы хотим обрести нормальное мышление, мы должны уйти из двузначного мира и освоить трехзначную логику в том виде, как ее создал Аристотель. Важно понимать, что, кроме ДА и НЕТ, есть еще и НЕ-ДА и НЕ-НЕТ. Если мы не хотим в школах воспитывать людей с рефлексами бюрократов и формалистов, то должны заменить двузначную логику трехзначной диалектической логикой Аристотеля»[13].

Да, чуть не забыл: единица информации в троичном компьютере – трит.

16 июля 2007–16 марта 2008

ПРОДОЛЖЕНИЕ СЮЖЕТА:

АЛЬТЕРНАТИВНЫЙ АЛГОРИТМ РЯДА ФИБОНАЧЧИ

И ОБОБЩЕННЫЙ АЛГОРИТМ ДЛЯ √2 И ЗОЛОТОГО СЕЧЕНИЯ