Андрей Чернов. Заметки о вечном

ИМХОТЕП = ХЕСИРА (3)

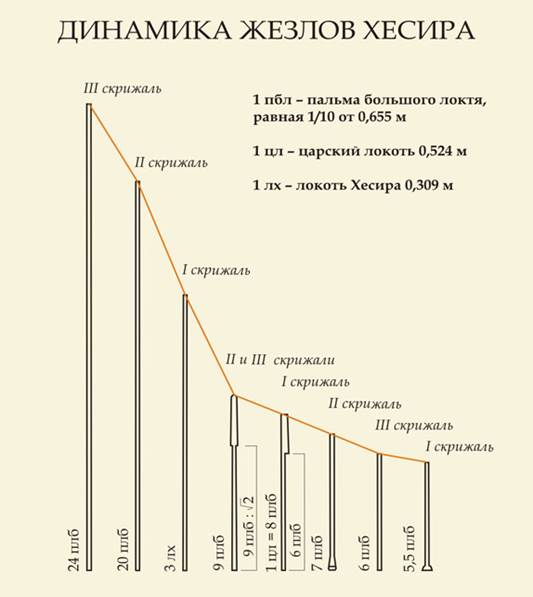
Можно предположить, что жезлов было десять, и резкий перепад графика между третьим и четвертым жезлами должен быть заполнен мерами в 17 и 12 пальм. Такое наблюдение подтверждается тем, что 17 к 12 – это неплохое целочисленное приближение к отношению диагонали квадрата и его стороне, а 12 к 9 (четвертый жезл) даст пропорции катетов священного египетского треугольника 4 к 3.

Однако достаточно и первой скрижали, чтобы попытаться понять тот канон, который заложен в мерах первого египетского зодчего. В царском локте и локте Хесира (лишь у греков эта мера станет футом, то есть длиной стопы) уже заложены все необходимые пропорции – от золотого сечения и корня из двойки до числа π. Надо было только догадаться разделить царский локоть не на 7, а на 8 пальм. (Впрочем, ситуация, скорее была обратной, и это позднейшее обожествление царского локтя привело к тому, что о нем мы знаем больше, чем о локте Хесира и большом локте)

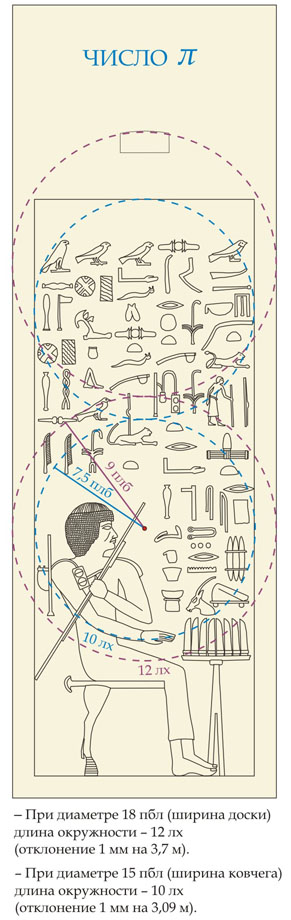
Само имя Хесира – не имя, а, скорее, жреческий сан (Посвященный Ра). Это то же, что «великий жрец Гелиополя» (вспомним, что в египетских текстах так именуется Имхотеп).

С точки зрения геометра у бога Ра, то есть Солнца, самая большая тайна – постоянство отношения длины окружности к диаметру. То есть число π.

Обнаружение этого числа в мерах Хесира могло бы быть случайностью, если б не одно обстоятельство: пропорции первой панели отличаются от пропорций других панелей, и виной тому именно π. Чтобы в этом убедиться, достаточно поставить ножку циркуля в ту точку, которую И. П. Шмелев назвал визиром.

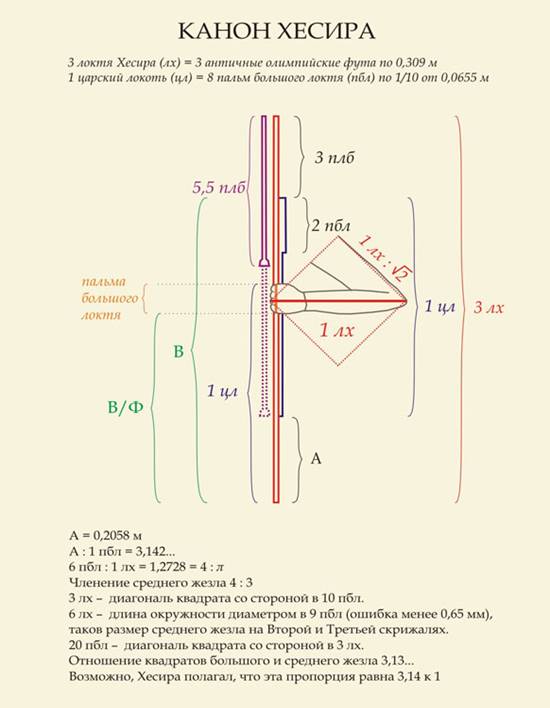
Итак, случайность исключена: дважды из одного центра мы получили две окружности, длины которых и диаметры могут быть выражены при помощи парной меры – большого локтя и локтя Хесира. Значит, локоть Хесира нужен не только как косая мера (диагональ квадрата), но и мера, через которую с хорошим приближением выражается число π.

Кроме того, на I скрижали мы видим прямоугольный треугольник, у которого гипотенуза равна царскому локтю, а малый катет локтю Хесира (их отношение практически равно двойному минорному золоту; отклонение 0,0016).

Древнейшее египетское упоминание о числе, которое мы сегодня записываем строчной греческой буквой π («пи»)[1], содержится в хранящемся сегодня в Британском музее в папирусе Ринда (по имени шотландского археолога Генри Александра Ринда, который обнаружил этот документ в 1855 году на теле одной из мумий). Папирус относится к Тринадцатой династии и датируется примерно 1700 годом до н. э., то есть написан через тысячу лет после сооружения пирамиды Хеопса, но писец Ахмес, утверждает, что переписал этот текст с оригинала двухсотлетней давности. В нем приводятся 84 задачи, в которых определяются площади прямоугольника, треугольника, трапеции и круга. Последняя приравнивается к площади квадрата со стороной в 8/9 диаметра, а это значит, что π равно 3,1605.

На этом основании делают вывод, что египтяне не знали более точного приближения к π. Но в данном случае речь лишь о самом простом и потому грубом приближении. Отмечено, что уникальность пирамиды Хеопса состоит в исключительной точности ориентации ее граней по сторонам света. Ошибка ничтожна: 0,00015. Если с такой же точностью египтяне высчитывали число π, то оно должно было бы равняться не 3,145, а 3,142, то есть совпадать с истинным до третьего знака по запятой.

Но зачем Хесира потребовалось число π?

Под пирамидой Джосера, в 1837 г. английский инженер и топограф Джон Перринг  обнаружил колодец – круглую трубу и глубиной 23,5  и диаметром 9 м (пропорция Ф² к 1). Под днищем колодца и располагалась запечатанная четырехтонным гранитным блоком погребальная камера. А над жерлом колодца – чуть приплюснутый полусферический купол, древнейший из купольных сводов человечества.

Вероятно, скрижали Хесира, как и план Великих пирамид в Гизе, содержат гораздо больше информации, чем мы полагаем. И прав Борис Раушенбах, заметивший, что египтяне не рисовали. А в чертеже самая малая малость может быть ключом к великой тайне. Для примера сошлюсь на такую мелочь, как число листьев у двух пальмовых ветвей в иероглифическом поле скрижалей Хесира, которое показывает, что зодчий знал и целочисленное приближение к √5 : 2.

Сегодня на человека, который шифрует свои знания подобным образом, посмотрят косо или даже намекнут, что ему не худо бы обратиться к доктору. Но то, что сейчас воспринимается как отклонение от нормы, в древности было нормой сакрального мышления: тотальная регламентация всей жизни диктовала и тотальную установку на детерминированность даже такой мелочи, как число листьев на ветвях иероглифа. Благодаря этому скрижали Хесира, план его мастабы, или разрез пирамиды Хеопса, являют нам код древнего знания в сверх-концентрированном виде. Другое дело, что лишь многократность повторения некоего мотива может служить гарантией того, что мы правильно прочитали код.

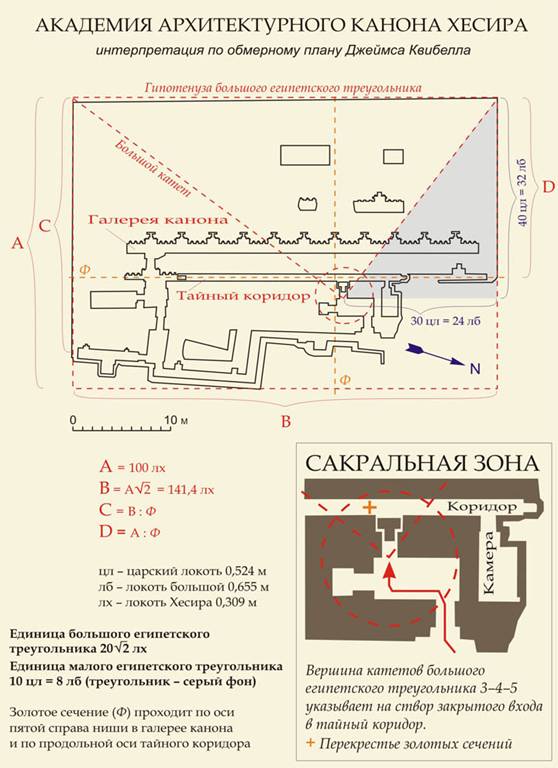
Храм Хесира в Саккаре (а это именно храм или, если угодно, – Академия архитектурного канона) вписан в прямоугольник √2 к 1 (где единица равна 100 локтям Хесира, то есть 100 единицам меры, обнаруженной мной на I скрижали Хесира). Это первая из фундаментальных пропорций Имхотепа, положенная в основу всего канона. Но торцевые стены (южная и северная) – золото величины относительно длинной и короткой сторон прямоугольника.

Это ясно из чертежа Джеймса Квибелла. Скопируем чертеж и интерпретируем его пропорции, вписав в план священный египетский треугольник 3–4–5.

О том, как работал зодчий, всегда помнит его постройка.

Пересечем прямоугольник плана диагоналями и получим точку, находящуюся на линии западной стены галереи канона. Здесь и были установлены скрижали. (И если б стены храма были стеклянными, их озаряло утреннее солнце.)

В храме длинный, хотя и не слишком сложный коридор ведет в галерею канона, а первый поворот направо приводит к мнимому тупику, за которым находится некий тайный коридор.

Меридиональная ось золотого сечения и проходит по оси тайного коридора.

Обратим внимание на то, как спроектирован план мастабы Хесира. От большого размера взят √2, а от полученного золотое сечение. Именно так спроектирован и план всего мемориального комплекса Джосера, где такая же цепочка задает длинный размер основания пирамиды. Это свидетельствует о том, что Хесира проектировал оба объекта, а, значит, Хесира и есть Имхотеп.

Вершина двух катетов священного египетского треугольника 3–4–5, находящаяся близ перекрестья двух линий золотого сечения, указывает на створ входа в тайный коридор. Вход перекрыт каменным блоком. Если его сдвинуть и пойти направо, после двенадцатифутового простенка (напомню, что локоть Хесира равен греческому футу) откроется вход в узкий и короткий коридорчик, из которого попадаешь в тесную камеру шириной 1,64 на 2,32 м (именно столько, сколько надо для скромного саркофага). Пропорции самой камеры – 1 к √2, а прибавленные к длине помещения два уступа коридорчика дадут по отношению к ширине камеры двойное мажорное и двойное минорное золото.

Можно предположить, что здесь находилось погребение Хесира.

Имхотеп был первым, кто начал строить пирамиды. Эта архитектурная форма родилась из того типа гробниц, который называется мастаба. Они появляются, когда египтяне научились бальзамировать умерших. У мастаб плоские кровли и чуть наклоненные внутрь стены. А в плане мастаба – прямоугольник. К подземной погребальной камере ведет наклонный коридор. Из коридора и можно попасть в сердаб – узкую камеру, где, питаясь изображенными на стенах яствами, продолжала жить бессмертная душа усопшего («Ка»). Впрочем, после похорон коридор засыпался песком. Рядом строили небольшую капеллу с ложной дверью – узкой щелью, ведущей в сердаб. Стены капеллы покрывали фрески и барельефы, рассказывающие о жизни покойного.

Имхотеп придумал поставить несколько мастаб друг на друга и получилась пирамида.

Тайная камера Хесира совсем рядом с входом в его мастабу. И если в галерею канона ведет лабиринт (хотя довольно простой), то в тайный коридор можно попасть из первого же, якобы ложного, кармана. Такая близость к миру едва не погубила само место упокоения архитектора. Храм частично разрушен, и самые значительные разрушения именно с северо-восточной его стороны, со стороны входа. Пала и одна из стен тайного коридора, но провал ведет в никуда: у тайного коридора тройная блокировка (с востока, юга и севера). Однако некогда трехметровая (в толщину) северная стена склепа сегодня похудела до сорока сантиметров.

Однако то, что каменные замки уцелели, а камера пуста, – многообещающий сюжет.

Не удивлюсь, если окажется, что склеп Хесира просто еще не найден. Судя по логике пропорциональных пристрастий зодчего, он должен быть не направо в двенадцати футах от входа в тайный коридор, а налево и ровно в три раза ближе. Там, где пересекаются две золотые горизонтали храма Имхотепа.

Археологи тоже ошибаются: геометрический т-образный монолит, запирающий вход в сакральную зону храма, отмечен на плане Квибелла, но не на плане Смита (1958 г.), у которого в этом месте изображена глухая стена. Видимо, осыпавшаяся за полвека кладка перекрыла это место. Но ведь и у Джеймса Квибелла не было георадара, и он также мог просто не заметить того, что искал всю свою жизнь.

Реконструируем систему египетских строительных мер.

ЕГИПЕТСКИЕ МЕРЫ ПО СКРИЖАЛЯМ ХЕСИРА И ПИРАМИДЕ ХЕОПСА

Большой локоть (в 10 пальм большого локтя) – 0,655 м

Царский локоть (7 классических пальм или 8 пальм большого локтя) – 0,524 м

Локоть (6 классических пальм) – 0,449 м

Локоть Хесира – 0,3087 м (через две с хвостом тысячи лет – античный олимпийский фут).

Стопа (1/2 царского локтя или фут в 4 пальмы большого локтя) – 0,262 м

Пальма большого локтя – 0,0655 м

Пальма классическая – 0,0749 м

Палец классический ( ¼ классической пальмы) – 0,0187 м

Итак, мы можем констатировать, что система строительных мер Хесира настроена на пропорцию гармонических парных мер: это сторона и диагональ квадрата (1 и Ö2), сторона и диагональ полуквадрата (1 и Ö5, а также производное от них – золотое сечение), длина окружности и ее диаметр (1 и 1/π).

Знал ли Хесира о квадратных корнях, то есть о тайне иррационального?  Само наличие парной меры свидетельствует, что знал. С диагоналями квадрата и полуквадрата (последняя относится к короткой стороне полуквадрата как √5 к 1) архитектору приходилось работать и в прохладе кабинета, и на жаркой (до +50 С⁰) строительной площадке. При помощи мотка упругой бечевы (чем не нить Ариадны?), медной линейки (человечество только что научилось плавить металл) и деревянного циркуля Хесира прошел над той иррациональной бездной, которая много позже поразила и напугала Пифагора. И именно потому египтяне почитали треугольник со сторонами 3–4–5 священным, что он-то и снимал проблему несоизмеримости.

Напомним, что от Хесира из его XXVIII в. до н. э. до Пифагора было почти так же далеко, как от Пифагора до нас.

Старый сфинкс из Саккары, отрытый полтора века назад Огюстом Мариетом, знал тайну эталона. И если молчание – золото, то в самой его немоте и скрыта подсказка.

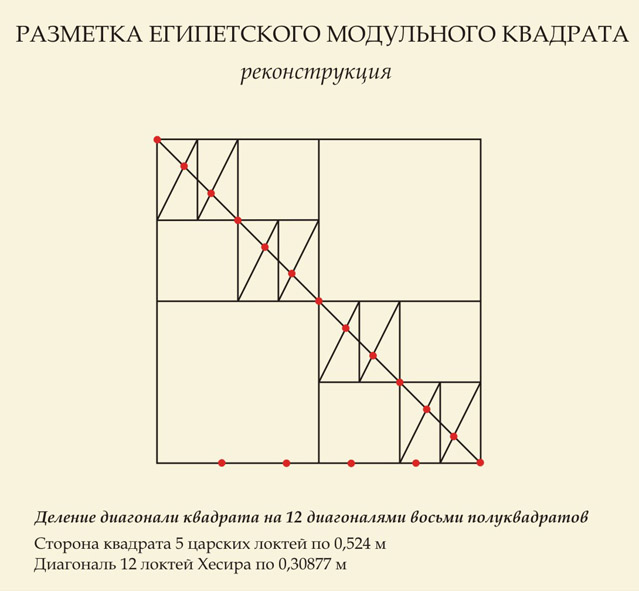
ЭВОЛЮЦИЯ МОДУЛЬНОГО КВАДРАТА

Для того, чтобы без ошибки разбить план основания пирамиды, египетские зодчие должны был пользоваться парной мерой (термин Иосифа Шевелева, введенный им на материале древнерусской архитектуры, но восходящий к наблюдению Б. А. Рыбакова о том, что две из древнерусских саженей были связаны с двумя другими как сторона и диагональ квадрата[2]). Так и в Египте в паре к царскому локтю должна была существовать некая диагональная мера. Эту вторую меру мне и удалось обнаружить на панелях из храма архитектора Хесира в Саккаре. Мы назвали ее локоть Хесира (лх). Реконструируем, как должен был выглядеть египетский модульный квадрат, сопрягающий две меры – сторону и диагональ квадрата.

Вдоль каждой из сторон основания пирамиды умещается по 88 модульных квадратов.

Самое удивительное, что величина локтя Хесира (а на панелях это именно локоть) до десятых долей миллиметра совпадает с античным олимпийским футом (им размерен Парфенон), который потом с византийскими зодчими придет на Древнюю Русь и станет 1/7 так называемой «большой сажени».

Это значит, что античные греки заимствовали свою меру у египтян, после передали Византии, а византийские строители принесли ее на Русь, где она сохранялась вплоть до конца XVII в. н. э., то есть до времени Алексея Михайловича Тишайшего. (Но о Древней Руси мы будем говорить в пятой главе этой книжки.)

Парной мерой будут пользоваться и в Греции, и в Риме. Покажем, что греческие олимпийский фут и дорический локоть, а также римский фут и римский локоть, – также меры, основанные на стороне и диагонали квадрата. 

В древности парная мера должна была объединять пропорцией два мерных эталона (иначе она просто бессмысленна). Это может быть сторона и диагональ полуквадрата, или одна из самых популярных античных пропорций: 9/4, то есть 2,25 к 1 – самое первое и самое простое целочисленное приближение к √5.

Но наиболее простой, а потому и базовой фигурой является квадрат.

Для того чтобы построить правильный квадрат, надо знать длину его диагонали, ведь если измерять лишь длину сторон, нельзя определить, что перед нами – квадрат или ромб.

Потому-то каждая «прямая» мера требует себе в пару меру «косую».

Реконструируем модульные квадраты Египта и античности.

ЗАМЕТКИ НА ПОЛЯХ

1. Самый простой и логичный модульный квадрат – квадрат Хесира, сторону которого составляет один большой локоть в 0,655 м, а диагональ – 3 локтя Хесира (по 0,30877 м).

Учетверенный вариант этого квадрата завязан на царский локоть.

2. 4 греческих дорийских локтя – 1,96 м (это в самом прямом смысле «краеугольный камень» Парфенона, ведь именно таков нижний диаметр угловой его колонны). Но в модульном квадрате с такой стороной диагональ равна 9 олимпийским футам.

4 ∙ 0,4903 м ∙ 17/12 : 9 = 0,30871 м

Если брать вместо 17/12 привычный нам √2, то длина фута будет 0,308173 м, но повторим: древние умели вычислять значения квадратных корней лишь по целочисленным приближениям. Следовательно, заимствовав у египтян локоть Хесира, греки также использовали его как диагональную меру, но при этом взяли в качестве диагонали квадрата девять локтей (по 0,30871 м), а потом разделили на 17/12 и еще раз на четыре. И получили величину дорийского фута. То есть они всего лишь целочисленно имитировали парную меру, по сути, сведя ее к одной. Но при этом настроили отношение локтя к футу на мажорное золото:

0,4903 м : 0,30871 м = 1,59 → Ф

3. Очевидно, что и римские меры устроены по тому же принципу модульного квадрата (а, точнее, – его целочисленной имитации). Древнеримский локоть равен 0,444 м, а фут 0,296 м. Это натуральное отношение 3 к 2. Для построения модульного квадрата надо взять 17 футов (диагональ), и 8 локтей (сторона). И эти величины будут относиться как 17 к 12, то есть как диагональ и сторона квадрата.

Римляне, люди сугубо рациональные, отступили от древних мер (но сохранили пропорцию диагонали к стороне в древнейшем ее понимании 17/12) для увеличения площади базового квадрата. Они свели отношение локтя к футу к отношению 3 : 2, то есть 1,5 к 1. И тем, по сути, отказались от парной меры. В Константинопольской Софии большинство базовых размеров можно интерпретировать одновременно и в римских футах, и в римских локтях. Скажем, диаметр подкупольного барабана 105 римских футов (рф), но одновременно это 70 римских локтей (рл), а диаметры малых куполов 21 рф или 14 рл.

Доказательством того, что модульные квадраты действительно существовали в таком виде является одинаковое целочисленное приближение к √2, связывающее олимпийский фут с дорическим локтем и римский фут с римским локтем. В обоих случаях это 17/12. Это говорит о том, что Греция и Рим не сами открыли парную меру, а заимствовали ее у египтян. Античные строители не возводили пирамид. Им это было неинтересно. Но, если бы они попытались повторить опыт предшествующей цивилизации и построить пирамиду Хеопса, у них бы ничего не получилось: при выражении корня из двойки через 17/12 диагональ была бы на 0,566 м длиннее геометрической. А, значит, ребра пирамиды в точке вершине просто бы не сошлись.

Любопытно однако, что римский модульный квадрат больше, чем даже египетский. Видимо, такова дань имперским амбициям.

1994–2008