|
Правка 5 мая 2009 Андрей Чернов ЗОЛОТО
ПАРФЕНОНА (3) глава из книги МАТРИЦА ЗОЛОТОГО
СЕЧЕНИЯ На потолочных плитах Парфенона был выгравирован орнамент с пропорциональной матрицей. В ней и следует искать разгадку мерных отношений храма.
ПАРФЕНОН.
МАТРИЦА ЗОЛОТОГО СЕЧЕНИЯ В центре матрицы довольно экзотические для Греции растения – цветок лотоса и метелка папируса. Цветок лотоса символизирует здесь сторону квадрата, а побег папируса – его диагональ (то есть прямую и “косую” меру). Высота стебля лотоса (от центра квадрата до бутона) равна высоте бутона. Вспомним, что Пифагор учился математике в Египте. Хотя рисунок оправлен меандром, то есть типично греческим орнаментом, растительные реалии свидетельствуют, что идею золотого сечения греки заимствовали у египтян. Тем более, что в Египте со времен V династии капители колонн делались или в виде лотоса, или в виде метелки папируса. Цветок лотоса был геральдическим знаком Верхнего Египта, а стебель папируса Египта Нижнего. Поэтому, надо думать, перед нами растиражированный в мраморе чертеж египетских жрецов.
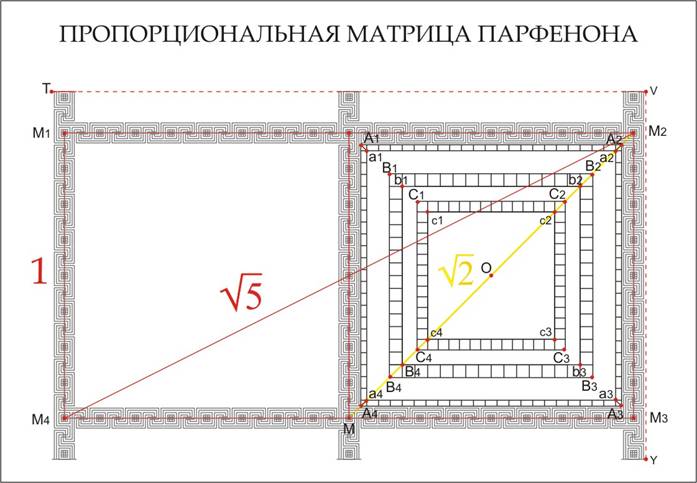
Рамой рисунку – меандровый орнамент. Всмотримся в его линии. Прямоугольник двойного квадрата (4 на 8 олимпийских футов) проходит по центру окаймляющего рисунок меандра. Вот как будет выглядеть матрица Парфенона, если оставить на чертеже лишь голую математику.
M1M2M3M4 – двойной квадрат 4 на 8 олимпийских
футов (8 на 16 шагов меандра). A1A2A3A4 – мерная линейка со шкалой в
2 дюйма (угловые квадратики по 1 дюйму). Длина стороны мерной линейки без двух
угловых квадратиков 7 шагов меандра или 3,5 оф. 8 светлых линий меандра – 3 дюйма, а
32 линии – 1 оф. Диагональ двойного квадрата (M2M4)
минус короткая его сторона (M2M3) равна двойному минорному золоту, то есть √5
– 1. Но такова величина диагонали квадрата мерной линейки, взятой без двух
угловых квадратиков (a2a4). Сторона более крупного квадрата становится
диагональю меньшего: a3a4 = b2b4 = 3,5 оф = 42 дюйма = 7 шагов меандра b1b2 = c2c4 = 2,5 оф = 30 дюйма = 5
шагов меандра c1c2 = Ob4 Отношение горизонтали к вертикали по
числу линий таково, что если размер брать по габаритным точкам T,V,Y, то
267 : 165 = 3 · (89 : 55) = 1,6182... Следовательно, TV : VY – целочисленное
приближение к золотому сечению через два смежных числа ряда Фибоначчи. Однако для того, чтобы ответить, как пользовались древние зодчие пропорциональной матрицей, нужны специальные разыскания и исследования. Шаг меандра (от одной крестчатой розетки до другой) в натуре равен ½ олимпийского фута. С внутренней стороны меандрового квадрата находится измерительная линейка со шкалой в два дюйма (угловые квадратики шкалы – по дюйму). Высота вертикальных мачт равна диагонали квадрата измерительной линейки. Короткая сторона меандрового прямоугольника равна диагонали среднего квадрата (взятой по внешней стороне рамы из стилизованных лепестков). Сторона малого квадрата (с рисунком внутри его) – диагональ среднего квадрата. (Внешняя сторона малой лепесковой рамы, в два раза меньше короткой стороны меандрового прямоугольника.) Внутренняя сторона большой лепестковой рамы – 0,62 от короткой стороны меандрового прямоугольника двойного квадрата, а внутренняя сторона малой лепестковой рамы – 0,62 от внутренней стороны большой лепестковой рамы. Отношение горизонтали меандра к его вертикали равно 1,6 к 1, а отношение ширины чертежа к высоте (с учетом «шрифтовых засечек» на концах вертикальных мачт) дает золотую пропорцию. Итак, мы убедились, что расчисленный парной мерой Парфенон, – это гимн иррациональному: квадратным корням и золотому сечению. Но имеет ли к этому какое-либо отношение скульптор Фидий? Очевидно, имеет. Внутри храма стояла двенадцатиметровая статуя Афины из золота и слоновой кости. Другая, бронзовая статуя Афины-Промахос (Воительницы) была чем-то вроде маяка находилась перед храмом. Моряки издалека видели, как горит копье и гребень шлема богини-девы. Увы, оба этих изваяния утрачены. А. В. Радзюкевич не нашел в наследии античности примеров членения человеческого тела по золотому сечению. Но обратимся к римской копии 1 в. до н. э., сделанной с оригинала другого греческого скульптора и современника Фидия – Мирона. В случае с Афиной Мирона золото и впрямь приходится на пряжку пояса богини, то есть на пупок. Может быть, потому, что на голове у Девы-воительницы высокий шлем.
Древнегреческую поговорку «В Афины со своей совой» (сова была символом Афины, а потому и носящего ее имя города) мы знаем по русской кальке «В Тулу со своим самоваром». Но есть и другая русская реплика на античный оригинал: «В чужой монастырь со своим уставом». Последнего сами греки не боялись. Они знали законы пропорции. Археологи обнаружили несколько античных пропорциональных циркулей. Один из них, помпейский, настроенный на золотое сечение, сегодня хранится в Неаполе. Его длина 14,6 см делится шарниром на отрезки 5,6 и 9 см. Три других циркуля найдены в Риме. Циркуль длиной 21,9 см разделен на отрезки 14,6 и 7,3 мм[1], а циркуль длиной 20,1 см на отрезки 13,4 и 6,7 см (оба настроены на пропорцию 2 к 1). Циркуль Музея Терм в Риме (14,6 см) разделен на отрезки 9,4 и 5,2 см, то есть, как показал И. Ш. Шевелев, установлен на отношение √5 : (√5 – 1).
Римская
арка императора Константина свидетельствует, что архитекторы античности
проектировали свои шедевры не на основе примитивной арифметики Витрувия, а по
корням из двойки и пятерки, золотому сечению и числу π. 2008 – 2009 Приложение 1. ПАРАМЕТРЫ И
ПРОПОРЦИИ ПАРФЕНОНА ОБЩИЕ РАЗМЕРЫ 1. Ширина стилобата (плита, на
которую опираются колонны) – 30,87 м = 100
оф = 63 дл Дорийский локоть в 0,4903 м вычислен не по √2, а по
целочисленному приближению к нему (17/12). В идеальном случае при 1оф = 0,30871 м он должен равняться 0,4912 м. 2. Средняя длина стилобата – 69,515 м 100 оф ×
2,25 = 69,46 м; (в натуре больше на 5,5 см) Альтернативный вариант вычисления через
дорийский локоть (0,4903 м): 63 дл = 30,89 см 100 дл ×
17/12 = 69,459 м; 63 дл ×
2,25 = 69,5 м; (в натуре больше на 1,5 см) 63 дл длинней 100 оф лишь на 1,8 см. Длина
стилобата могла быть расчислена и футом, и локтем. Видимо, именно это
сближение двух мер и привлекало строителей.
2. Ширина евтентерия – 33,96 м, то есть 110 оф. 3. Высота Парфенона (от нулевой отметки евтентерия) – ок. 19,94 м и высота фронтона ок. 4,32 м Верх фронтона разрушен, и обмерные чертежи
дают лишь предположительную величину, вычисляемую по углу схода кровли. Геометрически
высота фронтона с точностью до 3 см будет равна 4,32 м (но 4,322 м – 14 оф).
При этом высота фронтона с толщиной лежащего под ним карниза равна
рассчетному шагу рядовых колонн – 4,923 м. При таких величинах отношение
высоты храма к высоте верхней точки капители, взятой от нулевой отметки, дает
золотое сечение с точностью 1,619. А кроме того, высота каннелюров (колонна с
шейкой капители), деленная на 2,25, даст 14 оф, т. е. высоту фронтона
(погрешность 1,5 мм). 4. Вертикальный обмер от низа евтентерия до верха антаблемента: 1,887 м + 10,43 м + 3,297 м = 15,614 м Через двузначное приближение к √2
это можно выразить так: 2,25 × 10 дл ×
17/12 = 15,628 м КОЛОННА
1. Высота
ствола колонн – 9,570 м = 31 оф
Ширина стилобата 100 оф, а
100 : 31 есть целочисленное приближение к (√5 + 1).
(В дорийских локтях высота
ствола колонны Парфенона целочисленно не выражается.)
2. Высота капители – 0,86 м Высоту капители можно получить, построив
полуквадрат с короткой стороной в 2,25 оф (два фута и три дюйма при дюйме в
1/12 фута) и вычтя от длины его диагонали размер короткой стороны. Если
строить геометрически, то высота капители будет 0,859 м, но заменим
геометрическое построение алгебраическим: 1 оф ×
2,25 × 26/21 = 0,86 м 26/21 – одно из лучших приближений к √5
– 1 3. Высота колонны с капителью – 10,43 м 15 оф ×
2,25 = 10,419 м Откл. 11 мм 15 дл ×
17/12 = 10,419 м Откл. 11 мм 4. Высота эхина и абака (верхние части капители) – по 0,351 м Это высота капители, деленная на √5
– 1 0,86 м : 38/31 = 2 × 0,351 м 5. а) Ширина абака угловых колонн восточного фасада (навершие капители в виде прямоугольной доски) – 2,085 м 3 оф × 2,25 = 2,084 м Откл. 1 мм 3 дл × 17/12 = 2,084 м Откл. 1 мм И. Ш. Шевелев заметил, что ширина этих
абак равна 1/5 высоты колонны с капителью. б) Средняя ширина абак рядовой колонны восточного фасада – 2,058 м 15 оф : 2,25 = 2,058 м Откл. 0 6. Высота шейки капители – 0,158 м; высота тела колонны с ней 9,728 м 14 дл ×
17/12 = 9,724 м; Откл. 4 мм Высота тела колонны с шейкой капители
9,728 м. Умножим это число на 2,222… и получим ровно 70 оф (такой могла быть
высота фасада со скульптурной группой на фронтоне). 7. Нижний диаметр угловой колонны – 1,96 м. Это сторона модульного квадрата в 4 дорийских локтя. Угловые колонны толще рядовых. Это создает
иллюзию того, что колонны стоят по полуокружности, выгнутой своими краями
навстречу зрителю. Отношение диаметра угловой колонны к диаметру рядовой
колонны фасада равно пропорции живого ростового квадрата 1,03 к 1 8. Нижний диаметр рядовой колонны – 1,908 м 100 оф : 10Ф* = 1,908 м Ф* – целочисленное золотое приближение
55/34 9. Шаг рядовых колонн (пятикратно со второй по седьмую) – 4,295 м 10 оф
: Ф* × 2,25 = 4,294 м 10. Нижний диаметр колонн малых алтарей Парфенона – 0,442 м 1 оф, умноженный на 10/7 (целочисленное
приближение к √2) Откл. 1 мм ОРДЕР 1. Высота антаблемента + колонны с капителью – 13,728 м (28 дл). Высота колонны с капителью плюс антаблемент относится к высоте ствола колонны, взятой с шейкой капители (9,728) по √2 в целочисленном приближении 24/17. Но 16 оф ×
2,25× 21/17 =
13,7285 м АНТАБЛЕМЕНТ И ФРОНТОН 1. Высота антаблемента (карниз + фриз + архитрав) – 3,297 м 3 дл × 65/29
= 3,297; Откл. 0 где 65/29 – целочисленное приближение к √5 2.
Архитрав (1,35 м; прямоугольная балка, лежащая на колоннах) + фриз (1,347 м;
балка, лежащая между карнизом и архитравом) = 2,697 м 5,5 дл = 2,697 м 3. Высота карниза – 0,6 м. Расчет от архитрава: 1,35 м : 2,25 = 0,6 м; Откл. 0 5. Реконструированная высота фронтона – 4,322 м (14 оф) 6. От от нулевой отметки до низа подкарнизной балки (верхняя часть фриза) – 30 дл. Сумма высот от гребня кровли до низа подкарнизной балки (фронтон с кровлей + карниз + верхняя балка фриза) 5,212 м (это половина высоты колонны с капителью). СТЕРЕОБАТ 1. Высота стереобата (четыре ступени под колоннами) – 1,887 м (три верхних ступени – 1,592 м и евтентерий – 0,295 м) Метрологически эти размеры в целочисленном
виде не интерпретируются (6 оф + 0,02476 м). Это значит, что они получены
алгебраически. Так и оказывается: Стереобат + колонна с капителью ––––––––––––––––––––––––––––––– =
1,619 → Ф Антаблемент + фронтон При квадрате золотого сечения, равном
2,62: фронтон + карниз –––––––––––––––––
= 2,619 → Ф2 стереобат СВЯТИЛИЩЕ (НАОС) 1. Ширина наоса (внутреннее помещение) – 21,534 м 31 оф ×
2,25 = 21,532 м; Откл. 2 мм 31 дл ×
17/12 = 21,532 м; Откл. 2 мм 2. Длина наоса – 48,250 м
Отношение длины наоса к ширине = 2,2406 =
65/29 (с точностью 1 : 1,0002),
след., длина наоса равна ширине, умноженной на 65/29 (или 56/25): 31 оф × 2,25 × 65/29 = 48,263 м Приложение 2. ЦЕЛОЧИСЛЕННЫЕ ПРИБЛИЖЕНИЯ К
ИРРАЦИОНАЛЬНЫМ КОНСТАНТАМ Приближения к √2 = 1,4142136… 10 : 7 = 1,429 17 : 12 = 1,4167 24 : 17 = 1,412 41 : 29 = 1,4138 99 : 70 = 1,41429 100 : 71 = 1,41 Приближения к (√5 – 1) = 1,236068… 21 : 17 = 1,2353 27 : 22 = 1,2273… 31 : 25 = 1,24 38 : 31 = 1,226 100 : 81 = 1,235 Приближения к (√5 + 1) : 2 = 1,618034… (по числам ряда Фибоначчи) 8 : 5 = 1,6 13 : 8 = 1,625 21 : 13 = 1,615… 34 : 21 = 1,619… 55
: 34 = 1,6176…= Ф* 89 : 55 = 1,6182… 144 : 89 = 1,61798… 233 : 144 = 1,618056… Приближения к √3 = 1,732… 19 : 11 = 1,727272… 26 : 15 = 1,73333… Приближения к √5 = 2,236068… 9 : 4 = 2,25… 29 : 13 = 2,231… 38 : 17 = 2,2353… 47 : 21 = 2,238… 49 : 22 = 2,2273… 56 : 25 = 2,24… 65 : 29 = 2,241… 69 : 31 = 2,22581… 100 : 45 = 2,222… 181 : 81 = 2,235… Приближения к (√5 + 1) = 3,236068… 42 : 13 = 3,231… 55 : 17 = 3,2353… 68 : 21 = 3,238… 71 : 22 = 3,2273… 81 : 25 = 3,24… 94 : 29 = 3,241… 100 : 31 = 3,226… 262 : 81 = 3,235… |